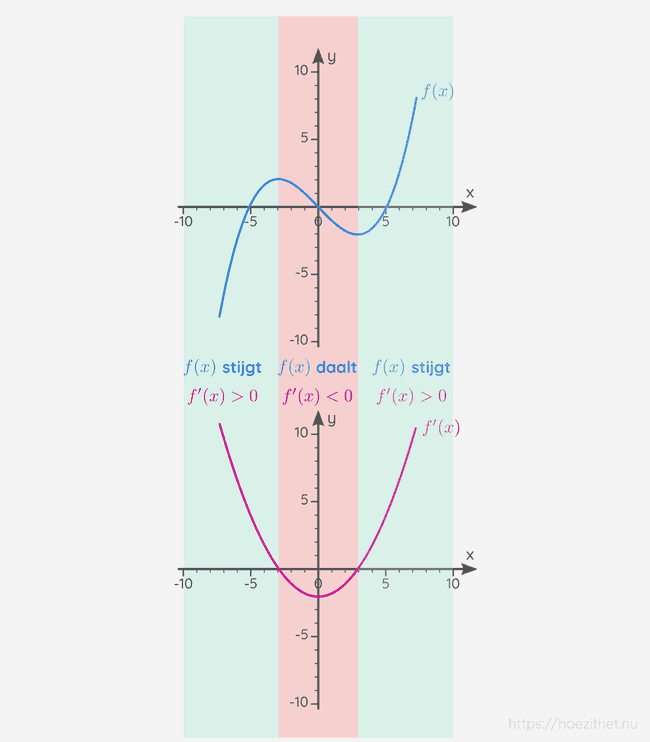
De grafiek van een afgeleide functie

Bron: https://hoezithet.nu/lessen/wiskunde/afgeleiden_1/grafiek/

In de les over de afgeleide functie leerden we hoe we de afgeleide van een volledige functie in één keer konden berekenen. Die afgeleide van een functie is zélf ook een functie. En van een functie kunnen we een grafiek tekenen.

In deze les leren we hoe je het verband kan zien tussen de grafiek van de afgeleide van een functie en de grafiek van de functie zelf.

Een grafiek vol met rico's

In de les over de afgeleide als rico van een raaklijn, hebben we gezien dat de afgeleide van een functie $f(x)$ in $x = a$ gelijk is aan de richtingscoëfficiënt van de raaklijn aan de grafiek van $f(x)$. Wanneer we dus voor een bepaalde x-waarde $x = a$ op de grafiek van $f'(x)$ gaan kijken naar de functiewaarde, is die functiewaarde de rico van de raaklijn aan de oorspronkelijke grafiek van $f(x)$ in $x = a$. Wanneer $f(x)$ stijgt, hebben de raaklijnen aan $f(x)$ een positieve rico en zal $f'(x)$ dus ook positief zijn. Wanneer $f(x)$ daalt, hebben de raaklijnen aan $f(x)$ een negatieve rico en zal $f'(x)$ dus ook negatief zijn.

Je kan de grafiek van $f'(x)$ dus zien als een verzameling van de rico's van alle raaklijnen aan de grafiek van $f(x)$ voor elke mogelijke x-waarde.