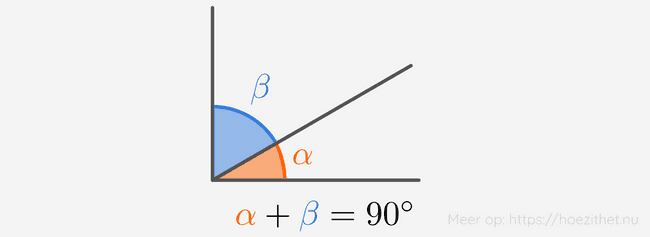Wat is een variabele?

Inhoud

Waarom hebben we variabelen nodig?
Altijd een element van een verzameling
Gebruik symbolen voor variabelen
Een variabele invullen
Samengevat

Pas wanneer een eenterm variabelen bevat, kunnen we eentermen gaan gebruiken in de echte wereld. Voor we eentermen zelf gaan bestuderen, is het dus belangrijk om te begrijpen wat variabelen juist zijn.

Waarom hebben we variabelen nodig?

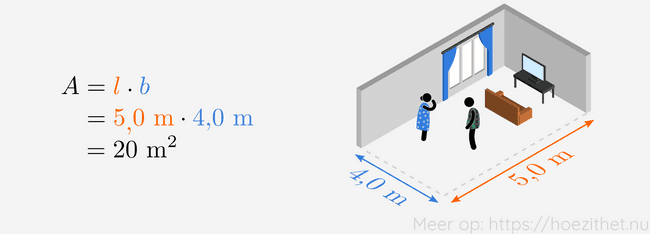
Mensen gebruiken dagelijks wiskunde om problemen op te lossen. Een heel eenvoudig voorbeeld is het berekenen van de oppervlakte van een rechthoek. Stel dat Maria en Dirk willen berekenen hoeveel tapijt ze in hun nieuwe rechthoekige living moeten leggen.

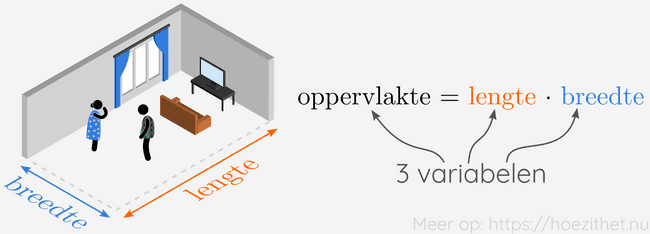
Dan moeten ze eerst weten wat de lengte en de breedte is van de living. Eens ze die gemeten hebben, vinden ze de oppervlakte als volgt:

\text{oppervlakte} = \orange{\text{lengte}}\cdot \blue{\text{breedte}}

En zonder dat we het goed en wel beseffen, hebben we maar liefst drie variabelen opgeschreven: $\text{oppervlakte}$ , $\orange{\text{lengte}}$ en $\blue{\text{breedte}}$ . De variabelen helpen ons om het verband tussen de lengte, breedte en oppervlakte van de living op te schrijven, zelfs wanneer Maria en Dirk nog niets gemeten hebben.

Het handige aan variabelen is dus dat je ze kan vervangen door verschillende mogelijke waarden.

Wanneer Maria en Dirk ook tapijt in hun rechthoekige slaapkamer willen leggen, zullen ze met dezelfde formule opnieuw de oppervlakte kunnen berekenen. Voor de variabelen maakt het niet uit dat hun slaapkamer andere afmetingen heeft dan hun living.

Altijd een element van een verzameling

Een variabele is dus iets wat je kan vervangen door van alles. Je kan een variabele echter niet door eender wat vervangen. Een variabele stelt altijd een element van een bepaalde verzameling voor.

De variabelen $\orange{\text{lengte}}$ en $\blue{\text{breedte}}$ , bijvoorbeeld, stellen afmetingen voor. Een afmeting is altijd een positief rationaal getal. Het kan bijvoorbeeld niet dat de lengte van de living een negatief getal zou zijn, zoals $-5{,}2~\si{m}$ . We zeggen dus dat de variabelen $\orange{\text{lengte}}$ en $\blue{\text{breedte}}$ elementen zijn van $\mathbb{Q}^+$ . Dat noteren we als volgt:

\begin{aligned} \orange{\text{lengte}} &\in \mathbb{Q}^+\\ \blue{\text{breedte}} &\in \mathbb{Q}^+\\ \end{aligned}

Hetzelfde geldt voor de oppervlakte, die ook een positief rationaal getal moet zijn:

\text{oppervlakte} \in \mathbb{Q}^+

Dat alles kunnen we korter schrijven als:

\text{oppervlakte},~\orange{\text{lengte}},~\blue{\text{breedte}} \in \mathbb{Q}^+

Gebruik symbolen voor variabelen

Het wordt lastig om altijd " $\text{oppervlakte}$ " , " $\orange{\text{lengte}}$ " en " $\blue{\text{breedte}}$ " te schrijven. Daarom gaan we onze variabelen afkorten. Dat kunnen we bijvoorbeeld doen met een letter, zoals $A$ voor de oppervlakte (van het Engelse "Area"), $\orange{l}$ voor de lengte en $\blue{b}$ voor de breedte. Onze formule wordt dan ook veel eenvoudiger om te schrijven:

A = \orange{l} \cdot \blue{b}

Een variabele stellen we zoals hierboven vaak voor met een letter. Soms gebruiken we ook Griekse letters zoals $\alpha$ , $\beta$ of $\gamma$ . Griekse letters gebruiken we voor bepaalde grootheden in de fysica zoals massadichtheid of in de meetkunde om hoeken aan te duiden.

Maar het hoeft natuurlijk niet altijd zo saai te zijn. Niets houdt je tegen om emoji's te gebruiken als variabele, zoals 🐶, 🐘 of 📏:

Een variabele invullen

Vanaf we de waarde van een variabele kennen, kunnen we die waarde gaan invullen. Dat betekent dat we de variabele vervangen door die waarde. Stel dat Maria en Dirk hun living hebben opgemeten en ze vinden een lengte van $\orange{5{,}0~\si{m}}$ en een breedte van $\blue{4{,}0~\si{m}}$ . Dan kunnen ze de variabelen $\orange{l}$ en $\blue{b}$ invullen in de formule voor de oppervlakte:

\begin{aligned} A &= \orange{l} \cdot \blue{b}\\ \Leftrightarrow A &= \orange{5{,}0~\si{m}} \cdot \blue{4{,}0~\si{m}}\\ \Leftrightarrow A &= 20~\si{m}^2 \end{aligned}

We vinden dat wanneer de variabele $\orange{l=5{,}0~\si{m}}$ en de variabele $\blue{b=4{,}0~\si{m}}$ , dat dan de variabele $A$ (de oppervlakte) gelijk is aan $20~\si{m}^2$ .

Samengevat

Een variabele stelt een element van een verzameling voor

Een variabele is een symbool dat een willekeurig element van een bepaalde verzameling voorstelt, zoals de natuurlijke of rationale getallen. Meestal gebruiken we letters zoals $a$ , $b$ en $c$ of $x$ , $y$ en $z$ als variabele.