Tekenschema

Inhoud

Tekenschema vanuit een grafiek
Tekenschema zonder grafiek
Enkel nulpunten en grenzen van domein
Samengevat

Naast het kennen van de nulpunten van een functie, is het ook vaak nuttig om te weten welke waarde we moeten kiezen voor $x$ zodat $f(x)$ positief of negatief is. Deze informatie vatten we overzichtelijk samen in een tekenschema.

Tekenschema vanuit een grafiek

Welke x-waarden welk teken (positief/negatief/nul) opleveren voor de y-waarden, vatten we samen in een tekenschema (ook wel "tekentabel" of "tekenverloop" genoemd). Als de grafiek van een functie is gegeven, kunnen we zien waar de functiewaarden (of de y-waarden) positief, negatief of nul zijn.

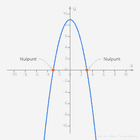
We zien op de grafiek:

Voor x-waarden kleiner dan $-3$ zijn alle y-waarden negatief;
Voor x gelijk aan $-3$ is de y-waarde nul;
Voor x-waarden tussen $-3$ en $3$ zijn alle y-waarden positief;
Voor x gelijk aan $3$ is de y-waarde nul;
Voor x-waarden groter dan $3$ zijn alle y-waarden negatief.

Dit vatten we als volgt samen in een tekenschema:

Ingang $x$	$-\infty$		$-3$		$3$		$+\infty$
Uitgang $y = f(x)$		$\red{-}$	$\blue{0}$	$\green{+}$	$\blue{0}$	$\red{-}$

Het schema toont:

Als de ingang ( $x$ ) iets tussen $-\infty$ en $-3$ is, is de uitgang ( $y$ ) negatief;
Als $x=-3$ , is $y$ nul;
Als $x$ iets tussen $-3$ en $3$ is, is $y$ positief;
Als $x=3$ is, is $y$ nul;
Als $x$ iets tussen $3$ en $+\infty$ is, is $y$ negatief.

Tekenschema zonder grafiek

We kunnen een tekenschema ook maken zonder een grafiek. Dit doen we in drie stappen.

Zet de grenzen van het domein in de bovenste rij van het tekenschema;
Zoek alle nulpunten en zet ze van klein naar groot (volgens x-waarde) tussen de grenzen van het domein;
Vind de tekens van $y$ tussen alle x-waarden in het schema (tenzij die x-waarden buiten het domein liggen).

We werken deze stappen uit voor de (reële) functie met voorschrift

f(x) = -x^2 + 9

Dit is de functie die hoort bij de grafiek van daarnet. We hopen dus ook hetzelfde tekenschema te krijgen.

Grenzen van het domein

We kunnen van eender welk reëel getal het kwadraat berekenen, dus we kunnen $f(x) = -x^2 + 9$ voor elk reëel getal $x$ berekenen. Dit betekent dat het domein van $f$ alle reële getallen bevat:

dom f = \mathbb{R}

Als interval geschreven is dit

dom f = \left] -\infty, +\infty \right[%]

De grenzen van het domein zijn dus $-\infty$ en $+\infty$ . Die zetten we op de bovenste rij van het tekenschema:

Ingang $x$	$-\infty$						$+\infty$
Uitgang $y = f(x)$

Nulpunten zoeken

We vinden de nulwaarden van de functie $f(x) = -x^2 + 9$ door de vergelijking

-x^2 + 9 = 0

op te lossen naar $x$ . Als je dat zou doen, vind je dat $x=-3$ en $x=3$ de nulwaarden zijn van deze functie $f$ . De nulpunten zijn dus $(-3,~\blue{0})$ en $(3,~\blue{0})$ . We zetten deze nulpunten gerangschikt in het tekenschema:

Ingang $x$	$-\infty$		$-3$		$3$		$+\infty$
Uitgang $y = f(x)$			$\blue{0}$		$\blue{0}$

Tekens van $y$ tussen alle x-waarden

Om het tekenschema te vervolledigen, moeten we op zoek naar welk teken er moet staan bij $y$ tussen alle x-waarden die in het schema staan. Dus tussen $-\infty$ en $-3$ , tussen $-3$ en $3$ , en tussen $3$ en $+\infty$ . Een trucje dat altijd werkt is:

Kies een eenvoudige x-waarde die ligt tussen de twee x-waarden;
Vul de gekozen x-waarde in in de functie;
Zet het teken van de uitkomst in het tekenschema.

Bijvoorbeeld het teken van $y$ voor $x$ tussen $-3$ en $3$ . Een eenvoudig getal dat ligt tussen $-3$ en $3$ is $0$ . Die vullen we in in $f(x) = -x^2 + 9$ :

f(\orange{0}) = -(\orange{0})^2 + 9 = \green{9}

We komen een positief getal uit, dus we zetten een $\green{+}$ tussen $-3$ en $3$ :

Ingang $x$	$-\infty$		$-3$		$3$		$+\infty$
Uitgang $y = f(x)$			$\blue{0}$	$\green{+}$	$\blue{0}$

Voor een x-waarde tussen $-\infty$ en $-3$ , kunnen we $-5$ nemen.

f(\orange{-5}) = -(\orange{-5})^2 + 9 = -25 + 9 = \red{-16}

Invullen geeft een negatief getal, dus we zetten een $\red{-}$ tussen $-\infty$ en $-3$ :

Ingang $x$	$-\infty$		$-3$		$3$		$+\infty$
Uitgang $y = f(x)$		$\red{-}$	$\blue{0}$	$\green{+}$	$\blue{0}$

Voor een x-waarde tussen $3$ en $+\infty$ , ten slotte, kunnen we $5$ nemen.

f(\orange{5}) = -(\orange{5})^2 + 9 = -25 + 9 = \red{-16}

Invullen geeft een negatief getal, dus we zetten een $\red{-}$ tussen $3$ en $+\infty$ :

Ingang $x$	$-\infty$		$-3$		$3$		$+\infty$
Uitgang $y = f(x)$		$\red{-}$	$\blue{0}$	$\green{+}$	$\blue{0}$	$\red{-}$

Et voilà! 💪 We krijgen hetzelfde tekenschema als daarnet.

Enkel nulpunten en grenzen van domein

De x-waarden die in een tekenschema staan (de bovenste rij), zijn ofwel nulwaarden ( $-3$ en $3$ in het vorige voorbeeld) ofwel grenzen van het domein ( $-\infty$ en $+\infty$ in het voorbeeld). Er zijn geen andere x-waarden nodig. Dat is omdat het teken van $y$ enkel kan veranderen na een nulpunt of na een grens van het domein.

Voor echt heel speciale functies kan het teken ook na andere x-waarden veranderen, namelijk na een discontinuïteit. Zulke functies zullen we niet zo vaak tegenkomen, dus is het niet de moeite om er nu verder op in te gaan. Zorgen voor later! 👋