Vectoren grafisch optellen
Inhoud
Vectoren kun je, net als getallen, bij elkaar optellen. Maar hoe gaat dat in zijn werk, zo pijlen bij elkaar optellen? In deze les leren we een manier om vectoren op te tellen via een tekening.
Verplaatsingen optellen
We zagen in een vorige les dat verplaatsing een vectoriële grootheid is. We zullen daarom eerst kijken wat een logische manier is om verplaatsingen bij elkaar op te tellen. Die manier zullen we dan veralgemenen naar alle vectoren.
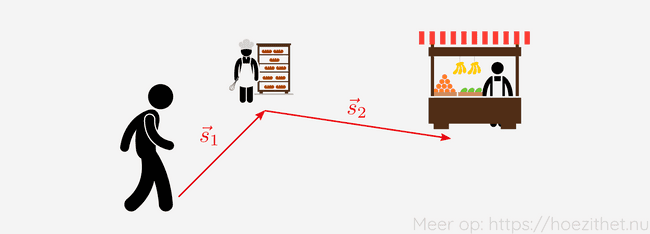
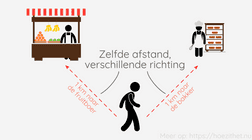
Stel dat we ons eerst verplaatsen naar de bakker en vervolgens naar de fruitboer. De eerste verplaatsing stellen we voor met vector en de tweede met vector .
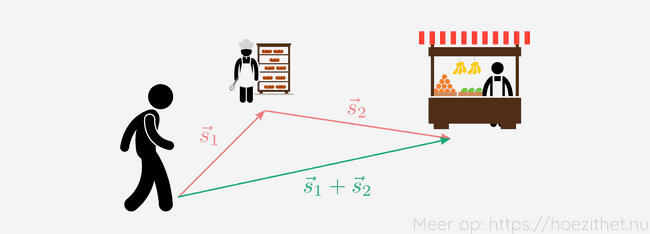
Aan welke vector is dan gelijk? Wel, we kijken waar we vertrokken zijn en tekenen een vector naar waar we geëindigd zijn. Dat is de som van de eerste verplaatsing en de tweede verplaatsing.
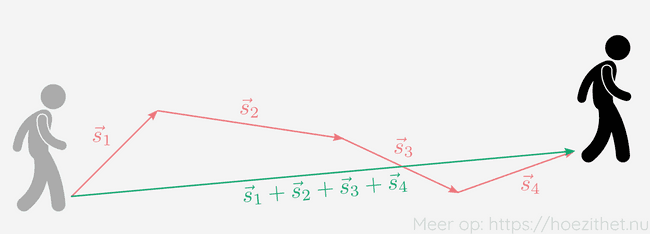
We hoeven ons natuurlijk niet te beperken tot twee verplaatsingen. De som van vier verplaatsingen , kunnen we op dezelfde manier doen. We kijken waar we begonnen zijn en tekenen een vector naar waar we eindigden.
Kop-staartmethode
Hierboven zagen we hoe we verplaatsingen kunnen optellen bij elkaar. Dit gaan we nu veralgemenen naar alle soorten vectoren, niet enkel verplaatsingen.
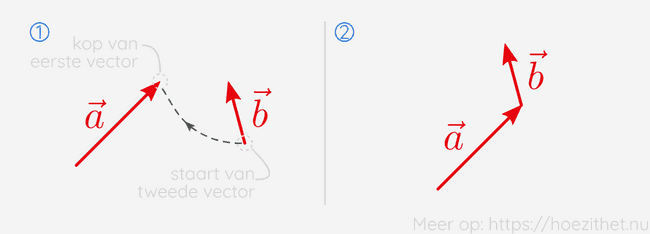
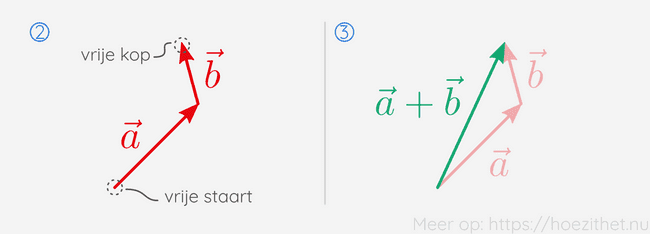
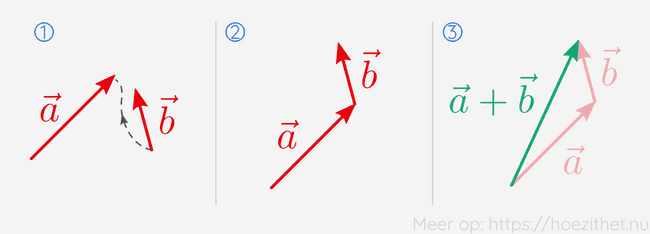
Als we twee vectoren willen optellen, plaatsen we de staart van de tweede vector aan de kop van de eerste.
Vervolgens tekenen we een vector van de vrije staart naar de vrije kop. Die vector is de som van de twee vectoren.
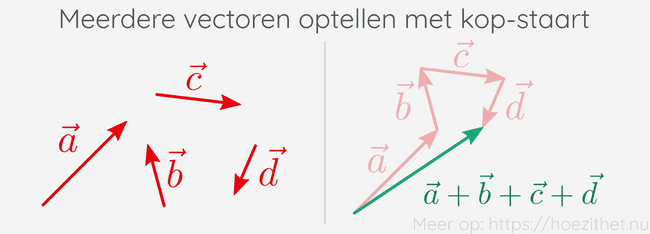
Dit kunnen we veralgemenen naar het optellen van meerdere vectoren. Eerst plaatsen we alle vectoren kop-staart-gewijs achter elkaar en vervolgens tekenen we een vector van de vrije staart naar de vrije kop.
Omdat we bij deze methode altijd een kop en een staart op elkaar leggen, noemen we dit de kop-staartmethode.
Parallellogram-methode
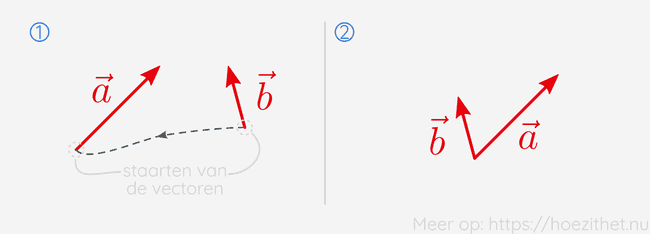
Het gebeurt vaak dat twee vectoren met de staarten bij elkaar liggen. We zouden dan een van de vectoren kunnen verleggen naar de kop van de andere om de kop-staartmethode toe te passen, maar het kan ook eenvoudiger.
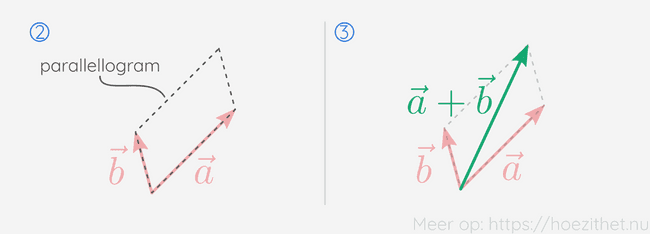
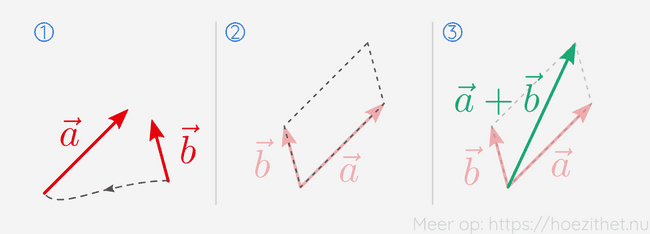
Bij de parallellogram-methode, krijgen we de som van twee vectoren door eerst de staarten op elkaar te leggen. Vectoren liggen echter al vaak met de staarten op elkaar, dus deze stap is niet altijd nodig.
Vervolgens maken we een parallellogram van de vectoren. We krijgen de som van de vectoren door een vector te tekenen die vertrekt vanuit de staarten en eindigt in de vrije hoek van het parallellogram.
Wanneer we meer dan twee vectoren willen optellen met de parallellogram-methode, moeten we eerst de eerste twee vectoren optellen, vervolgens de uitkomst met de volgende vector optellen enzovoort. Dat wordt al snel veel werk. De parallellogram-methode is dus vooral handig wanneer je maar twee vectoren wilt optellen die al met de staarten bij elkaar liggen.
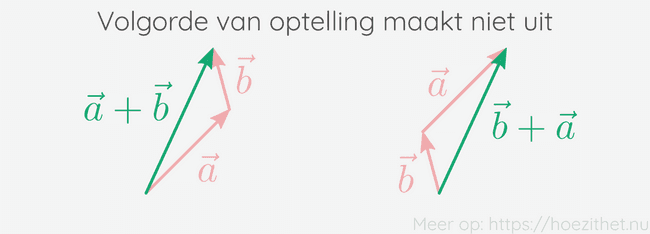
De volgorde van optellen maakt niet uit
Wanneer je vectoren bij elkaar optelt, maakt het niet uit in welke volgorde je die optelling doet. Dit kan het eenvoudigste geïllustreerd worden met de kop-staartmethode.
Mat andere woorden is het optellen van vectoren commutatief.
Samengevat
Kop-staartmethode
Bij de kop-staartmethode tekenen we de som van twee vectoren door de staart van de ene vector aan de kop van de andere te leggen. Vervolgens tekenen we een vector van de vrije staart naar de vrije kop.
Parallellogram-methode
Bij de parallellogram-methode tekenen we de som van twee vectoren door de staarten van de vectoren op elkaar te leggen. Vervolgens maken we een parallellogram van de vectoren en tekenen we een vector van de staarten naar de vrije hoek van het parallellogram.
Hoe duidelijk vond je deze les?
