Wat is een vector?
Inhoud
Over cijfers en getallen heb je al heel veel gehoord in je lessen wiskunde. Je had het misschien niet gedacht, maar wiskunde gaat niet enkel over getallen. Naast getallen, zijn er bijvoorbeeld ook vectoren, en die zijn minstens even belangrijk.
Een vector is een pijl
Een vector is niet meer dan een rechte pijl.
We geven vectoren vaak een naam, zoals vector en vector . Merk op dat we een pijltje zetten boven de naam van een vector.
| Schrijf | Lees |
|---|---|
| De vector | |
| De vector |
Een vector heeft een grootte, een richting en een zin
Vectoren hebben drie eigenschappen: een grootte, een richting en een zin. Als twee vectoren dezelfde grootte, richting en zin hebben, dan zijn die vectoren gelijk. De volgende twee vectoren, zijn bijvoorbeeld gelijk:
De grootte van de vector is hoe lang de vector is. De grootte van een vector is altijd positief. We noteren de grootte van een vector als of ook wel gewoon als (geen pijltje op de ).
| Schrijf | Lees |
|---|---|
| De grootte van | |
| De grootte van |
De volgende twee vectoren, hebben een verschillende grootte, en zijn daarom niet gelijk aan elkaar:
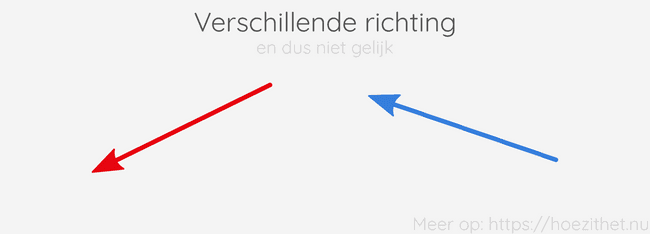
De richting van een vector zegt aan welke rechte de vector evenwijdig is. Bijvoorbeeld: "verticaal", of "horizontaal", of "onder een hoek van ". De vectoren in de onderstaande illustratie, hebben een verschillende richting, en zijn daarom niet gelijk aan elkaar.
De zin van een vector zegt naar welke kant de vector wijst. Dat kan bijvoorbeeld "naar links", "naar rechts", of "naar beneden" zijn. De volgende twee vectoren, hebben een verschillende zin, en zijn daarom niet gelijk aan elkaar:
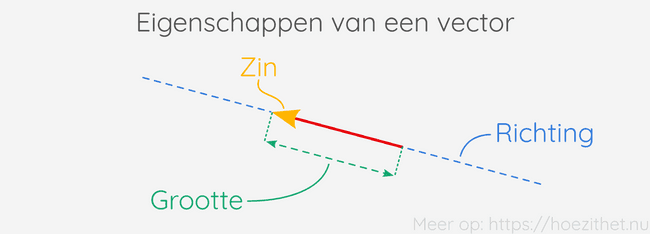
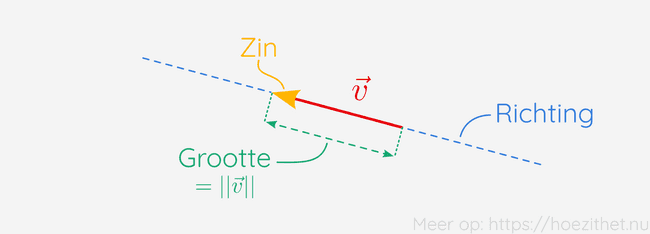
Deze figuur toont de drie eigenschappen van een vector samen:
Waarom toch?
Het is heel normaal als je je op dit moment afvraagt: "Waarom, in godsnaam, zijn die pijlen zo belangrijk?" Er zijn heel veel verschillende redenen waarom vectoren belangrijk zijn. Een van de meest voor de hand liggende redenen is dat veel grootheden in de fysica zich gedragen als vectoren omdat ze ook een grootte, een richting en een zin hebben.
Positie, verplaatsing, snelheid, kracht en versnelling zijn bijvoorbeeld allemaal vectoriële grootheden. In de volgende les gaan we iets dieper in op vectoriële grootheden.
Er zijn echter nog vele andere toepassingsgebieden van vectoren, maar daar kunnen we helaas hier niet verder op in gaan. Enkele voorbeelden: special effects in films, video games, stelsels van vergelijkingen oplossen, artificiële intelligentie...
Samengevat
Een vector is een pijl met een grootte, richting en zin