Vectoriële grootheden
Inhoud
In de vorige les leerden we dat vectoren pijlen zijn met een grootte, een richting en een zin. Na die les ben je misschien nog niet volledig overtuigd dat vectoren wel degelijk nuttig zijn. Daarom tonen we in deze les een voorbeeld van hoe vectoren kunnen voorkomen in de echte wereld.
Vectoriële grootheden hebben een richting en een zin
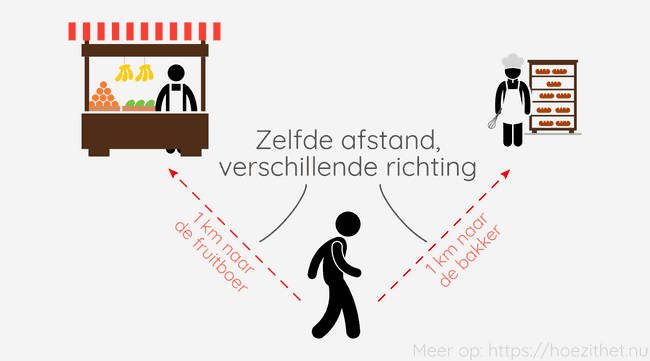
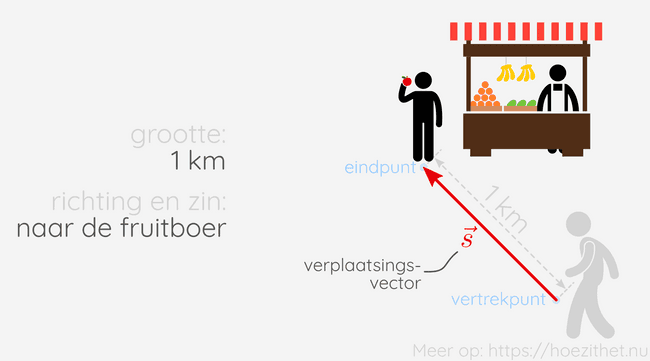
Vectoriële grootheid hebben altijd een richting en een zin. Verplaatsing, bijvoorbeeld, is een vectoriële grootheid. Als je alleen de afstand kent die iemand heeft afgelegd, kan je niet exact weten waar die persoon is geëindigd. Je moet niet alleen weten hoe ver de persoon is gestapt, je moet ook weten waarheen.
Hoe ver de persoon stapte, noemen we de grootte van de verplaatsing. Waarheen de persoon stapte, is de richting en de zin van de verplaatsing.
Andere voorbeelden van vectoriële grootheden zijn o.a. snelheid, versnelling en kracht.
Scalaire grootheden hebben géén richting
Er zijn natuurlijk ook veel grootheden die geen richting hebben. Hoeveel kilogram je weegt (je massa), heeft geen richting. Je kan bijvoorbeeld niet "80 kg naar links" wegen, maar wel gewoon "80 kg". Ook temperatuur heeft geen richting. "20 °C naar boven", bestaat niet, maar gewoon "20 °C" wel.
We noemen temperatuur en massa daarom scalaire grootheden. Ze hebben enkel een getalwaarde (scalar = getal). We kunnen geen vectoren gebruiken om de grootheden te beschrijven.
Samengevat
Vectoriële en scalaire grootheden
Vectoriële grootheden zijn grootheden die naast een grootte ook een richting en een zin hebben.
Scalaire grootheden hebben enkel een grootte.