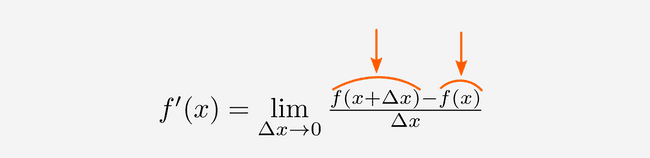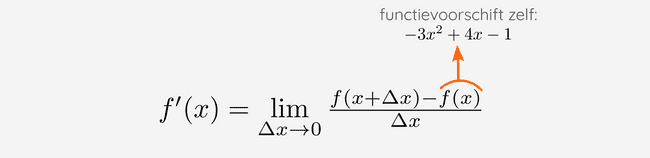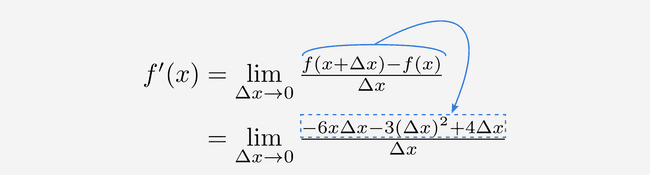De afgeleide van een functie

Bron: https://hoezithet.nu/lessen/wiskunde/afgeleiden_1/afgeleide_functie/

In de vorige les zagen we hoe je de afgeleide voor een bepaalde x-waarde van een functie $f(x)$ kan berekenen. Lees die les zeker eens na als je nog niet goed begrijpt wat we daar juist mee bedoelen. Je kan in die les zien dat het eigenlijk nogal veel werk is om zo'n afgeleide te berekenen. Zeker als we voor meerdere x-waarden die afgeleide zouden willen berekenen.

Gelukkig kunnen we ook de afgeleide van een volledige functie berekenen. Dat betekent dat we in één keer in alle x-waarden (waarin $f(x)$ afleidbaar is) de afgeleide berekenen! 😮 Dat noemen we de afgeleide functie van een functie of kortweg de afgeleide van een functie.

De afgeleide functie $f'(x)$

Met de afgeleide functie van een functie kunnen we heel snel de afgeleide vinden voor eender welke x-waarde waarin onze functie afleidbaar is. De afgeleide functie duiden we aan door een accent naast de $f$ van onze functie te zetten:

De afgeleide functie geeft ons een nieuw functievoorschrift $f'(x)$. In dat voorschrift kunnen we dan weer x-waarden invullen, net zoals we in $f(x)$ x-waarden kunnen invullen. Als we in $f'(x)$ een x-waarde invullen, berekenen we meteen de afgeleide van $f$ in die x-waarde. Zo moeten we niet telkens al het werk herhalen van de vorige les.

De afgeleide van een tweedegraadsfunctie

We hebben al geleerd dat een afgeleide functie $f'(x)$ ons veel werk kan besparen. Eens we $f'(x)$ gevonden hebben, kunnen we er namelijk eender welke x-waarde (waarin $f(x)$ afleidbaar is) in invullen en vinden we meteen de afgeleide in die x-waarde. Maar hoe vinden we die afgeleide functie? Als voorbeeld zoeken we in deze paragraaf de afgeleide functie van de volgende tweedegraadsfunctie:

We leerden in de vorige les hoe je in een bepaalde x-waarde de afgeleide kan berekenen. Daarvoor vulden we de x-waarde in in de definitie van een afgeleide. Nu doen we hetzelfde, maar in plaats van een bepaald getal in te vullen, vullen we nu $x$ in.

Herinner je de definitie van de afgeleide van $f(x)$ in $a$:

Lees zeker onze introductie tot afgeleiden eens na als je die formule niet zo goed begrijpt. Wij zijn nu op zoek naar de afgeleide functie van een functie, en dat is niet $f'(\blue{a})$, maar wel $f'(\blue{x})$. We moeten in onze definitie van $f'(a)$ de $a$ dus gewoon vervangen door een $x$:

En zo hebben we de definitie van de afgeleide functie van $f(x)$! 🙌 Als we naar die definitie kijken, zien we dat er twee keer iets met $f(\ldots)$ staat. De eerste keer staat er $f(x + \Delta x)$ en de tweede keer staat er $f(x)$:

Die $f(x + \Delta x)$ en $f(x)$ moeten we bepalen voor de functie waar we de afgeleide van willen vinden. Wij zoeken de afgeleide van $f(x) = -3x^2 + 4x - 1$, dus die $f(x)$ in de definitie kunnen we al meteen vervangen:

Maar hoe vinden we die vreemde $f(x + \Delta x)$? Daarvoor moeten we eigenlijk gewoon alle $x-$en in het functievoorschrift $f(x) = -3x^2 + 4x - 1$ vervangen door $(x + \Delta x)$:

We hebben nu $f(x + \Delta x)$ en $f(x)$ gevonden voor de functie die we willen afleiden. Nu moeten we alles uitwerken en de limiet uitrekenen. Om alles een beetje verteerbaar te houden, gaan we die harige $f(\blue{x + \Delta x})$ eerst apart uitwerken:

Die $f(x + \Delta x)$ blijft een serieus harige uitdrukking... 🙄 Als je terug even naar boven gaat, zie je in de definitie van $f'(x)$ in de teller van de breuk "$f(x + \Delta x) - f(x)$" staan. We moeten van onze $f(x + \Delta x)$ dus nog $f(x)$ aftrekken. Gelukkig vallen er dan een hele hoop dingen weg:

We hebben nu dus de teller gevonden van onze limiet:

Nu zou het je moeten opvallen dat er heel vaak in de breuk een $\Delta x$ staat. Het is zelfs zo dat elke term in de breuk een factor $\Delta x$ bevat. Dat betekent dat we de breuk kunnen vereenvoudigen door teller en noemer te delen door $\Delta x$.

Dat ziet er al een heel stuk properder uit! 😀 Het enige wat ons nu nog rest is de limiet zelf berekenen. De limiet zegt enkel iets over $\Delta x$, dus elke term zonder $\Delta x$ mogen we buiten de limiet zetten. Dan wordt de limiet heel eenvoudig en komt de afgeleide functie van $f(x) = -3x^2 + 4x - 1$ tevoorschijn!

Ziezo! We hebben de afgeleide functie $f'(x)$ gevonden! 💪

Hoe helpt een afgeleide functie ons nu?

Eens we $f'(x)$ gevonden hebben, kunnen we de afgeleiden van $f(x)$ in eender welke x-waarde (waarin $f(x)$ afleidbaar is) berekenen! In de vorige les hebben we bijvoorbeeld de afgeleide van de functie $f(x) = -3x^2 + 4x -1$ in $x=2$ berekend. Dat vergde toen heel wat werk om te vinden dat $f'(2)=-8$. Nu kunnen we dezelfde afgeleide veel sneller berekenen omdat we nu weten dat $f'(x) = -6x + 4$:

We kunnen nu heel snel ook andere afgeleiden berekenen:

Sneller de afgeleide functie vinden

Eens we de afgeleide functie hebben gevonden, kunnen we snel afgeleiden vinden in verschillende x-waarden. Maar we moeten toegeven dat het vinden van de afgeleide functie zelf wel nog steeds flink wat werk was. Gelukkig bestaan er voor heel wat functies binnenwegen om in één oogopslag de afgeleide te vinden. Hier leren we later meer over!

Samengevat