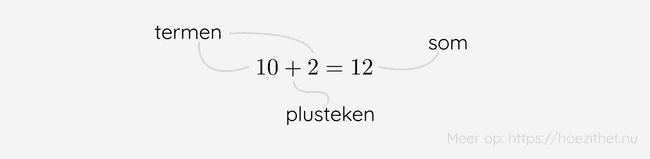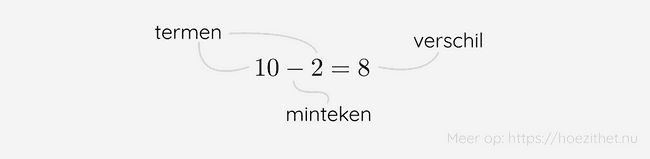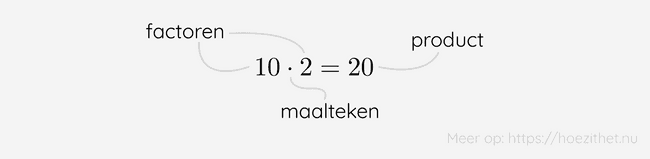De basisbewerkingen van de gehele getallen
Bron: https://hoezithet.nu/lessen/wiskunde/rekenen_rationaal/rekenen_gehele_getallen/
Alvorens we in de rationale getallen duiken, frissen we graag nog eerst even de bewerkingen met gehele getallen op. De verzameling van de gehele getallen (afgekort: ), kent vier basisbewerkingen: de optelling, de aftrekking, de vermenigvuldiging en de deling. We bespreken hieronder de terminologie en de eigenschappen van elk van deze basisbewerkingen. We gaan telkens ook wat dieper in op wat we moeten doen wanneer we in die bewerkingen negatieve getallen tegenkomen.
Gehele getallen optellen
Wanneer we getallen bij elkaar optellen, noemen we die getallen de termen van de optelling. De uitkomst van de optelling noemen we de som.
Een optelling voorstellen op een getallenas
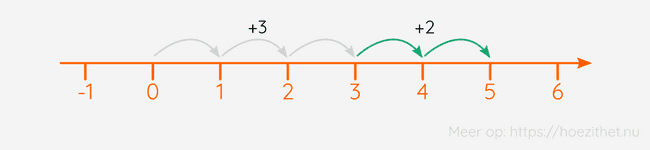
Een optelling kunnen we visueel voorstellen op een getallenas. We beginnen op de van de getallenas en telkens we een optelling tegenkomen, zetten we een aantal stappen. Wanneer je bv. vanaf de drie stappen naar rechts gaat en je daarna nog eens twee stappen naar rechts gaat, kom je uit op de van de getallenas. We kunnen dit schrijven als de som .
Optellingen met negatieve getallen
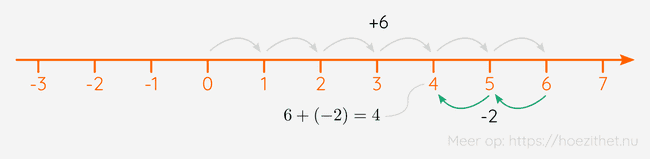
In de verzameling van de gehele getallen zitten er ook negatieve getallen. Hoe kunnen we die optellen? Een negatief getal optellen, betekent op onze getallenas dat we dat aantal stappen naar links zetten, in plaats van naar rechts. Zo krijg je wanneer je en optelt. Je gaat eerst zes stappen naar rechts en dan twee stappen naar links, door het minteken voor de .
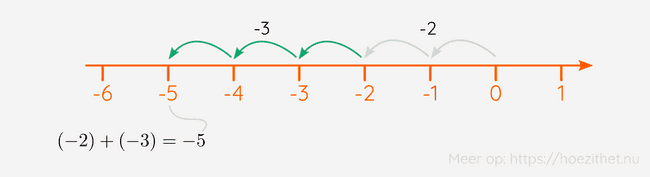
Je kunt natuurlijk ook twee negatieve getallen bij elkaar optellen. Zo krijg je wanneer je en optelt: je zet eerst twee stappen naar links en vervolgens nog eens drie stappen naar links.
De optelling in is commutatief
Of je nu eerst stappen naar rechts en vervolgens stappen naar rechts zet, of eerst stappen en dan stappen, dat maakt geen verschil:
We mogen dus de termen in een optelling van plaats veranderen. Wanneer de volgorde van het uitrekenen van een bewerking niet uitmaakt, zeggen we dat die bewerking commutatief is. Het optellen van gehele getallen is dus commutatief. Een ander voorbeeld:
Je ziet, onafhankelijk van de volgorde van de termen krijgen we steeds dezelfde oplossing.
De optelling in is associatief
Wanneer er haakjes in een bewerking staan, betekent het dat we eerst moeten uitrekenen wat er binnen de haakjes staat. Bijvoorbeeld
Dan moeten we eerst de die tussen de haakjes staat uitrekenen om vervolgens de volledige uitkomst te berekenen:
Maar wat als de opgave als volgt was?
Dan moeten we eerst de uitrekenen:
En wat zien we?! We krijgen dezelfde uitkomst! Zelfs wanneer we de haakjes helemaal weglaten, krijgen we dezelfde uitkomst:
Het maakt voor de optelling van de gehele getallen niet uit waar er haakjes staan. We zeggen dat de optelling van gehele getallen associatief is. Een ander voorbeeld:
Merk op dat de haakjes rond de niets met associativiteit te maken hebben. Die staan er enkel zodat het minteken niet zou "botsen" met het plusteken. Anders zouden we iets krijgen als en dat leest moeilijk. Veel properder (en juister) is .
Nul is het neutraal element voor de optelling in
Wanneer we ergens op de getallenas staan en we zetten nul stappen naar rechts, dan blijven we natuurlijk op hetzelfde getal staan. Enkele voorbeelden:
Nul optellen bij een getal geeft als uitkomst dus dat getal zelf. Ook als we bij nul een getal optellen, krijgen we het getal zelf:
We zien dat een optelling bij nul of een optelling met nul geen effect heeft. Daarom zeggen we dat nul het neutraal element is voor de optelling van gehele getallen.
Gehele getallen aftrekken
De onderdelen van een aftrekking noemen we, net als bij een optelling, de termen. Tussen die termen noteren we een minteken en de uitkomst van de aftrekking is het verschil.
Wanneer de aftrekking bestaat uit twee termen, noemen we de eerste term ook wel het aftrektal en de tweede term de aftrekker. In de aftrekking hierboven is dus het aftrektal en is de aftrekker.
Net zoals bij een optelling, kunnen we ook een aftrekking voorstellen op een getallenas. Het minteken zegt dat we voor het daarop volgende getal naar links moeten in plaats van naar rechts. Zo betekent : zet stappen naar rechts en vervolgens naar links, door het minteken voor de . We komen dan uit bij .
Aftrekkingen met negatieve getallen
Wat als we nu een negatief getal willen aftrekken? Bijvoorbeeld:
We zetten eerst stappen naar rechts, maar wat dan? stappen naar rechts of naar links? Één minteken wil zeggen: "naar links". Twee mintekens wil terug zeggen: "naar rechts". Dus: stappen naar rechts en vervolgens stappen opnieuw naar rechts. We komen uit op :
Merk op dat dit hetzelfde is als:
We zeggen dat twee opeenvolgende mintekens hetzelfde is als één plusteken. Vind je dat vreemd? We zullen even proberen uitleggen waarom dat eigenlijk logisch is. Een minteken betekent niets meer dan "het tegengestelde van":
- is het tegengestelde van
- is het tegengestelde van
- is het tegengestelde van
Als we nu twee opeenvolgende mintekens hebben, zoals bv. , dan kunnen we dat lezen als: "het tegengestelde van ". En dat is terug zelf natuurlijk.
Enkele andere voorbeelden:
- Het tegengestelde van is , dus
- Het tegengestelde van is , dus
- Het tegengestelde van is , dus
Wanneer we nu een aftrekking met een negatief getal tegenkomen, is het dus niet verwonderlijk dat dat neerkomt op een optelling:
Wat als dat eerste getal nu ook negatief is? Bijvoorbeeld,
Wel, dan doen we precies hetzelfde. De wordt terug en we krijgen de optelling van een negatief en positief getal:
Dat lezen we als: "We gaan eerst stappen naar links en vervolgens stappen naar rechts". We komen dan uit op :
Enkele andere voorbeelden:
De aftrekking in is NIET commutatief
In tegenstelling tot de optelling van gehele getallen, is de aftrekking van gehele getallen NIET commutatief! We mogen de termen van een aftrekking niet zomaar van plaats veranderen. Bijvoorbeeld:
Je ziet dat we niet dezelfde uitkomst hebben wanneer we de en de van plaats verwisselen.
De aftrekking in is NIET associatief
Ook de haakjes mag je niet zomaar van plaats veranderen bij een aftrekking. De aftrekking van gehele getallen is dus NIET associatief. Bijvoorbeeld:
Je ziet dat we niet dezelfde uitkomst hebben wanneer we de haakjes van plaats veranderen.
Een aftrekking omzetten naar een optelling
Het is je misschien al opgevallen dat bijvoorbeeld dezelfde uitkomst heeft als :
Dat is niet toevallig. Je kunt een aftrekking altijd herschrijven als een optelling. Dat is heel handig, want daardoor krijgen we ook alle eigenschappen van een optelling. Wanneer je een aftrekking herschrijft als een optelling, kan je de termen wél van plaats veranderen. Dat kan niet bij een aftrekking.
Dat maakt het soms ook eenvoudiger om uit te rekenen. Vanaf in gedachten stappen naar links zetten is moeilijker dan vanaf in gedachten stappen naar rechts te zetten.
Het omzetten van een aftrekking naar een optelling, is heel eenvoudig. Je zet het getal met het minteken tussen haakjes en zet een plusteken voor de haakjes. Enkele voorbeelden:
Gehele getallen vermenigvuldigen
De onderdelen van een vermenigvuldiging noemen we de factoren. Tussen de factoren noteren we een maalteken en de uitkomst van de vermenigvuldiging is het product.
Een vermenigvuldiging is eigenlijk een manier om een optelling van dezelfde getallen korter te schrijven.
Je zou kunnen lezen als: "zet keer stappen naar rechts". Dan heb je in totaal stappen naar rechts gezet, dus .
Plus maal min is min
Waaraan denk je dan dat gelijk is? Wel, je kunt lezen als "zet keer stappen naar links". (Naar links omdat er een minteken voor de staat.) Je hebt dan in totaal stappen naar links gezet, dus dat is hetzelfde als .
Wanneer we een positief en negatief getal met elkaar vermenigvuldigen, gaat de uitkomst altijd negatief zijn. Hetzelfde geldt trouwens voor het vermenigvuldigen van een negatief en positief getal. Enkele voorbeelden:
Daarom zeggen we: plus maal min is min. Een positief en een negatief getal vermenigvuldigen (of omgekeerd), geeft een negatieve uitkomst.
Min maal min is plus
Wanneer we echter een negatief en een ander negatief getal vermenigvuldigen, zal de uitkomst altijd positief zijn. Daarom zeggen we: min maal min is plus. Enkele voorbeelden:
Een beetje vreemd dat twee keer min plotseling plus geeft, niet? Hoe komt dat? Wel, je kunt het zien alsof "min maal min" het tegengestelde is van "plus maal min", net zoals het tegengestelde is van .
Probeer even mee te volgen. Het tegengestelde van
is dus (let op het minteken voor de ):
De uitkomst van moet dan ook het tegengestelde zijn van de uitkomst van . We weten al dat
De uitkomst van moet dus het tegengestelde zijn van . En dat is !
Kort gezegd: min maal min is plus!
Plus maal plus is plus
Om ons verhaal compleet te maken, vermelden we nog even iets wat je natuurlijk al wist: plus maal plus is plus. Enkele voorbeelden:
Dat zijn vermenigvuldigingen die je (hopelijk) al vaak bent tegengekomen.
Een gedurig product uitwerken
Hierboven leerden we de volgende rekenregels:
- Plus maal min is min
- Min maal plus is min
- Min maal min is plus
- Plus maal plus is plus
Er zijn twee zaken lastig aan deze vier rekenregels:
- Vier rekenregels onthouden is veel...
- We kunnen de rekenregels enkel toepassen als de vermenigvuldiging bestaat uit twee factoren.
Gelukkig is er ook één algemene rekenregel die we met eender welk aantal factoren kunnen toepassen! 🎉 Die rekenregel luidt als volgt:
Als er een even aantal mintekens staat in een vermenigvuldiging, is de uitkomst positief.
Als er een oneven aantal mintekens staat in een vermenigvuldiging, is de uitkomst negatief.
Stel bijvoorbeeld dat we de volgende vermenigvuldiging moeten uitrekenen:
Dat is een voorbeeld van een gedurig product. Dat is een product dat bestaat uit meer dan twee factoren. Hoe kunnen we de uitkomst van dit gedurig product uitrekenen?
Wel, ten eerste staan er drie mintekens. Er staat dus een oneven aantal mintekens in de vermenigvuldiging. De uitkomst zal dus negatief zijn. Eens we het teken kennen, moeten we enkel nog de absolute waarde van de uitkomst berekenen. Dat doen we door de absolute waarde van de getallen zelf te vermenigvuldigen: . De uitkomst van bovenstaande vermenigvuldiging is dus:
Om een gedurige som uit te rekenen neem je dus de volgende stappen:
- Bepaal het teken van de uitkomst door het aantal mintekens te tellen. Een even aantal mintekens betekent een positieve uitkomst; een oneven aantal betekent een negatieve uitkomst.
- Bereken de absolute waarde van de uitkomst door alle getallen te vermenigvuldigen zonder rekening te houden met het teken. Je vermenigvuldigt dus de absolute waardes.
Een ander voorbeeld:
- Bepaal het teken: We zien twee mintekens. Er staat dus een even aantal mintekens in de vermenigvuldiging. De uitkomst zal dus positief zijn
- Bereken de absolute waarde:
De uitkomst is dus:
De vermenigvuldiging in is commutatief
Net zoals de optelling van gehele getallen, is ook de vermenigvuldiging van gehele getallen commutatief. Dat betekent dat de volgorde van de factoren niet uitmaakt. Bijvoorbeeld:
De vermenigvuldiging in is associatief
De vermenigvuldiging van gehele getallen is ook associatief. Dat betekent dat de positie van de haakjes niet uitmaakt. Bijvoorbeeld:
is het neutraal element voor de vermenigvuldiging in
Er bestaat ook een neutraal element voor de vermenigvuldiging van gehele getallen. Dat is , want als je een getal met vermenigvuldigt, is de uitkomst gelijk aan dat getal zelf. Enkele voorbeelden:
Ook wanneer je vermenigvuldigt met een getal, is de uitkomst dat getal zelf:
Nul is het opslorpend element voor de vermenigvuldiging in
Een speciale eigenschap van de vermenigvuldiging is dat wanneer er een factor voorkomt, die alle andere factoren opslorpt en de uitkomst gewoon gelijk is aan . We zeggen daarom dat het opslorpend element is voor de vermenigvuldiging van gehele getallen. Enkele voorbeelden:
De vermenigvuldiging in is distributief ten opzichte van het optellen en aftrekken
De laatste eigenschap van de vermenigvuldiging van gehele getallen zegt dat deze distribrutief is ten opzichte van het optellen en aftrekken. Wat betekent dat nu? Wel, distribueren betekent eigenlijk uitdelen, denk maar aan het Engelse werkwoord "to distribute". De distributieve eigenschap betekent dan ook dat wanneer je een getal vermenigvuldigt met een optelling (of aftrekking), je dat getal mag uitdelen aan elk van de termen van die optelling (of aftrekking).
Stel bijvoorbeeld dat we de volgende vermenigvuldiging moeten uitrekenen:
De eerste manier om dit uit te rekenen, is door eerst gewoon uit te rekenen wat er tussen de haakjes staat. Dan maken we geen gebruik van de distributieve eigenschap.
Een tweede manier is om wél gebruik te maken van de distributieve eigenschap en de factor uit de delen aan elke term van de optelling. We zien dat we dezelfde uitkomst krijgen:
Let wel goed op met mintekens wanneer je de distributieve eigenschap toepast. Zorg dat de factor die je uitdeelt mooi zijn teken meeneemt en dat je ook het teken van de termen opnieuw schrijft:
Het kan natuurlijk ook dat de factor na de haakjes staat:
Gehele getallen delen
Een deling bestaat uit een deeltal die we moeten delen door een deler. Het resultaat van een deling noemen we het quotiënt.
Een deling als kan je lezen als: "Als ik bolletjes in gelijke groepen wil verdelen, hoeveel bolletjes zitten er dan in elk groepje?" Dat is in dit geval .
Delen met negatieve getallen
Om een deling met negatieve getallen uit te rekenen, moeten we net als bij de vermenigvuldiging eerst op zoek naar het teken van de uitkomst. Gelukkig zijn de rekenregels heel gelijkaardig als bij de vermenigvuldiging:
- Plus gedeeld door min is min
- Min gedeeld door plus is min
- Min gedeeld door min is plus
- Plus gedeeld door plus is plus
Of, in één regeltje: een even aantal mintekens in de deling geeft een positieve uitkomst; een oneven aantal mintekens in de deling geeft een negatieve uitkomst.
Eens we het teken van de uitkomst hebben bepaald, berekenen we de waarde van de uitkomst door de absolute waarden van de opgave te delen.
Enkele voorbeelden:
- (plus gedeeld door min)
- (min gedeeld door plus)
- (min gedeeld door min)
- (plus gedeeld door plus)
De deling van gehele getallen is NIET commutatief
Je kunt het deeltal en de deler van een deling niet zomaar van plaats verwisselen. De deling van gehele getallen is dus niet commutatief. Een voorbeeld:
Je ziet dat we niet dezelfde uitkomst krijgen wanneer we het deeltal en de deler omwisselen.
De deling van gehele getallen is NIET associatief
Je kunt ook de haakjes niet zomaar van plaats veranderen bij een deling van gehele getallen. De deling van gehele getallen is dus niet associatief. Een voorbeeld:
Je ziet dat we niet dezelfde uitkomst krijgen wanneer we de haakjes in de deling van plaats veranderen.
Samengevat
Basisbewerkingen
De verzameling van de gehele getallen kent vier basisbewerkingen:
- De optelling: bestaat uit termen en geeft een som als resultaat.
- De aftrekking: bestaat uit een aftrektal en een aftrekker (of ook gewoon "termen") en geeft een verschil als resultaat.
- De vermenigvuldiging: bestaat uit factoren en geeft een product als resultaat.
- De deling: bestaat uit een deeltal en een deler . Het resultaat noemt men het quotiënt.
Eigenschappen van de optelling van gehele getallen
- De optelling in is commutatief:
- De optelling in is associatief:
- is het neutraal element voor de optelling in :
Teken van een vermenigvuldiging
Bij een vermenigvuldiging geldt:
- Plus maal min is min
- Min maal plus is min
- Min maal min is plus
- Plus maal plus is plus
Of algemener:
- Als er een even aantal mintekens staat in een vermenigvuldiging, is de uitkomst positief.
- Als er een oneven aantal mintekens staat in een vermenigvuldiging, is de uitkomst negatief.
Eigenschappen van de vermenigvuldiging van gehele getallen
De vermenigvuldiging in is commutatief:
De vermenigvuldiging in is associatief:
is het neutraal element voor de vermenigvuldiging in :
is het opslorpend element voor de vermenigvuldiging in :
De vermenigvuldiging in is distributief over de optelling in :
De vermenigvuldiging in is distributief over de aftrekking in :
Teken van een deling
Bij een deling geldt:
- Plus gedeeld door min is min
- Min gedeeld door plus is min
- Min gedeeld door min is plus
- Plus gedeeld door plus is plus
Of algemener:
- Als er een even aantal mintekens staat in een deling, is de uitkomst positief.
- Als er een oneven aantal mintekens staat in een deling, is de uitkomst negatief.