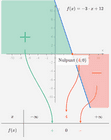
Het voorschrift van een eerstegraadsfunctie opstellen

Inhoud

De rico en een punt op de grafiek zijn gegeven
Twee punten op de grafiek zijn gegeven
Verschillende manieren waarop punten en rico gegeven kunnen zijn
Samengevat

Iedere eerstegraadsfunctie kunnen we schrijven als

f(x) = mx + q

waarbij $m\in\RR_0$ en $q\in\RR$ . Om het voorschrift van een eerstegraadsfunctie te vinden, moet je te weten komen waaraan $m$ en $q$ gelijk zijn. Hiervoor heb je altijd twee gegevens nodig:

ofwel de richtingscoëfficiënt van de functie en een punt dat op de grafiek van de functie ligt;
ofwel twee punten die op de grafiek van de functie liggen.

We bespreken in de volgende paragrafen hoe je in beide situaties het voorschrift kan vinden.

De rico en een punt op de grafiek zijn gegeven

Stel dat we het voorschrift van een eerstegraadsfunctie moeten vinden waarvan de rico gelijk is aan $-3$ en waarvan de grafiek door het punt $(2, 1)$ gaat. We weten dat het voorschrift van een eerstegraadsfunctie er als volgt uit ziet:

f(x) = mx + q

Waarbij $m$ de rico is en $q$ de y-coördinaat van het snijpunt met de y-as. In de opgave staat dat de rico gelijk is aan $-3$ . We kunnen $m$ dus al meteen vervangen door de gegeven rico:

f(x) = \orange{-3} x + q

Om $q$ te vinden, vullen we het gegeven punt in in het voorschrift. Als het punt $(2, 1)$ op de grafiek van $f$ ligt, dan betekent dit dat $f(2)=1$ . We vervangen $x$ in het voorschrift door $2$ . De uitkomst hiervan moet gelijk zijn aan $1$ :

\begin{aligned} f(\orange{2}) &= -3\cdot\orange{2} + q = \orange{1}\\ \end{aligned}

Hieruit volgt de vergelijking

\begin{aligned} -3\cdot\orange{2} + q &= \orange{1}\\ \end{aligned}

Dit is een vergelijking van de eerste graad die we kunnen oplossen naar $q$ :

\begin{aligned} -3\cdot2 + q &= 1\\ &\Udarr\\ -6 + q &= 1\\ &\Udarr\\ q &= 1 + 6\\ &\Udarr\\ q &= 7 \end{aligned}

We zien dat $q=7$ . Uit de gegevens wisten we ook dat $m=-3$ . Met deze $m$ en $q$ kunnen we nu dus het voorschrift van $f$ opstellen:

f(x) = \orange{-3}x + \orange{7}

Klaar! 🥳

💡 Functievoorschrift van een eerstegraadsfunctie bepalen wanneer de rico en een punt op de grafiek zijn gegeven

Wanneer de rico van een functie gegeven is, samen met een punt dat op de grafiek van die functie ligt, dan kan je het voorschrift van die functie als volgt vinden:

Vervang de $m$ in $f(x) = mx + q$ door de gegeven rico.
Vul de x-coördinaat van het punt in in dit voorschrift en stel dit gelijk aan de y-coördinaat van het punt. Werk deze vergelijking uit naar $q$ .
In stap 1 vond je $m$ , in stap 2 vond je $q$ . Vervang $m$ en $q$ in $f(x) = mx + q$ door de gevonden waarden en je krijgt het voorschrift! 🙌

Oefening NaN

Wat is het functievoorschrift van de eerstegraadsfunctie die door het punt

(6;4)

gaat en waarvan de richtingscoëfficiënt gelijk is aan

-3

(Noteer je antwoord zelf op papier.)

Twee punten op de grafiek zijn gegeven

Wanneer er twee punten gegeven zijn die op de grafiek van $f$ liggen, moeten we eerst de rico van de functie berekenen. In onze les over de richtingscoëfficiënt leerden we dat de rico van de functie die door de punten $(x_1, y_1)$ en $(x_2, y_2)$ gaat gelijk is aan:

m = \frac{y_2 - y_1}{x_2 - x_1}

Stel dat we het voorschrift zoeken van de functie die door de punten $(2, 4)$ en $(-2, 6)$ gaat. Dan is de rico van deze functie gelijk aan:

\begin{aligned} m &= \frac{6 - 4}{-2 - 2}\\ &= \frac{2}{-4}\\ &= -0{,}5 \end{aligned}

We vinden een rico $m=-0{,}5$ . Nu we de rico kennen, kunnen we gewoon de stappen volgen uit de vorige paragraaf! We vullen eerst de gevonden rico in in het voorschrift:

f(x) = \orange{-0{,}5}x + q

Vervolgens vullen we de x-waarde van een van de gegeven punten in en stellen dit gelijk aan de bijhorende y-waarde. Het maakt niet uit welk punt je kiest, je zal voor beide punten dezelfde uitkomst vinden (controleer dit maar!). We kiezen bijvoorbeeld punt $(2, 4)$ :

f(\orange{2}) = -0{,}5\cdot\orange{2} + q = \orange{4}

Hieruit volgt de vergelijking:

-0{,}5\cdot 2 + q = 4

Deze vergelijking kunnen we oplossen naar $q$ :

\begin{aligned} -0{,}5\cdot 2 + q &= 4\\ &\Udarr\\ -1 + q &= 4\\ &\Udarr\\ q &= 4 + 1\\ &\Udarr\\ q &= 5\\ \end{aligned}

We vinden dat $q=5$ en krijgen dus het voorschrift:

f(x) = -0{,}5x + 5

Je ziet dat, eens we de rico hebben gevonden, we eigenlijk juist hetzelfde doen als in de vorige paragraaf.

💡 Functievoorschrift van een eerstegraadsfunctie bepalen wanneer twee punten op de grafiek zijn gegeven

Wanneer twee punten $(x_1, y_1)$ en $(x_2, y_2)$ op de grafiek liggen van een functie, dan kan je het voorschrift van die functie als volgt vinden:

Bereken de rico met behulp van de twee gegeven punten: $m = \frac{y_2 - y_1}{x_2 - x_1}$ .
Kies een van beide punten en gebruik dit samen met de rico om dezelfde stappen te volgen als wanneer de rico en een punt zijn gegeven.

Oefening NaN

Wat is het functievoorschrift van de eerstegraadsfunctie die door de punten

(9;3)

(0;7)

gaat?

(Noteer je antwoord zelf op papier.)

Verschillende manieren waarop punten en rico gegeven kunnen zijn

Voor het bepalen van het voorschrift van een eerstegraadsfunctie heb je altijd ofwel een rico en een punt ofwel twee punten nodig. Soms zitten deze gevens echter wat verstopt in de opgave.

Enkele voorbeelden van hoe de richtingscoëfficiënt gegeven kan zijn:

Als de x-waarde 5 eenheden vergroot, dan verlaagt de functiewaarde met 2 eenheden: de rico van de functie is $\frac{-2}{5}$ ;
De functiewaarde vergroot met $5$ y-eenheden per x-eenheid: de rico van de functie is $5$ ;
De functiewaarde verkleint met $4$ y-eenheden per x-eenheid: de rico van de functie is $-4$ .

Enkele voorbeelden van hoe een punt op de functie gegeven kan zijn:

De nulwaarde van de functie is $-8$ : het punt $(-8, 0)$ ligt op de grafiek van de functie;
De functie snijdt de y-as in y-waarde $3$ : het punt $(0, 3)$ ligt op de grafiek van de functie;
$q$ in het functievoorschrift is $3$ : het punt $(0, 3)$ ligt op de grafiek van de functie;
De functie snijdt de x-as in x-waarde $-1$ : het punt $(-1, 0)$ ligt op de grafiek van de functie;
Bij x-waarde $-2$ is de y-waarde $7$ : het punt $(-2, 7)$ ligt op de grafiek van de functie.

Samengevat

💡 Functievoorschrift van een eerstegraadsfunctie bepalen wanneer de rico en een punt op de grafiek zijn gegeven

Wanneer de rico van een functie gegeven is, samen met een punt dat op de grafiek van die functie ligt, dan kan je het voorschrift van die functie als volgt vinden:

Vervang de $m$ in $f(x) = mx + q$ door de gegeven rico.
Vul de x-coördinaat van het punt in in dit voorschrift en stel dit gelijk aan de y-coördinaat van het punt. Werk deze vergelijking uit naar $q$ .
In stap 1 vond je $m$ , in stap 2 vond je $q$ . Vervang $m$ en $q$ in $f(x) = mx + q$ door de gevonden waarden en je krijgt het voorschrift! 🙌

💡 Functievoorschrift van een eerstegraadsfunctie bepalen wanneer twee punten op de grafiek zijn gegeven

Wanneer twee punten $(x_1, y_1)$ en $(x_2, y_2)$ op de grafiek liggen van een functie, dan kan je het voorschrift van die functie als volgt vinden:

Bereken de rico met behulp van de twee gegeven punten: $m = \frac{y_2 - y_1}{x_2 - x_1}$ .
Kies een van beide punten en gebruik dit samen met de rico om dezelfde stappen te volgen als wanneer de rico en een punt zijn gegeven.