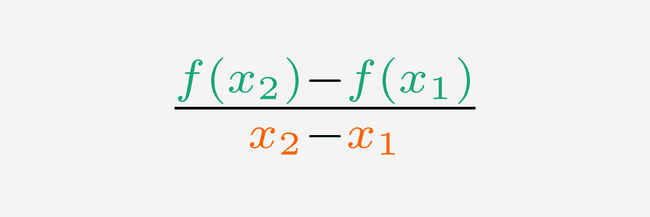Wat is een differentiequotiënt?

Inhoud

Gemiddelde snelheid als een breuk van twee verschillen
Gemiddelde snelheid veralgemenen naar het differentiequotiënt
Het verschil korter schrijven
Samengevat

Vooraleer we aan afgeleiden kunnen beginnen, moeten we het differentiequotiënt begrijpen. Wat een monster van een woord! 🦕 Maar geen paniek. We gaan het stap voor stap uitleggen aan de hand van iets waar je wel al ervaring mee zal hebben: het berekenen van de gemiddelde snelheid.

Gemiddelde snelheid als een breuk van twee verschillen

Maria houdt van dragracen. Bij een dragrace vertrekken twee wagens vanuit stilstand en racen ze $300~\si{m}$ in een rechte lijn. De eerste aan de finish wint.

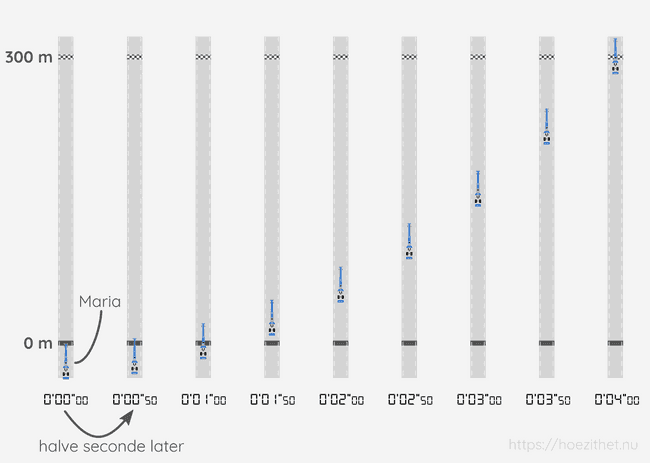
De wagens halen enorme snelheden tot meer dan $500~\si{km/h}$ . Hieronder zie je enkele luchtfoto's van Maria in haar Top Fuel dragster tijdens het dragracen.

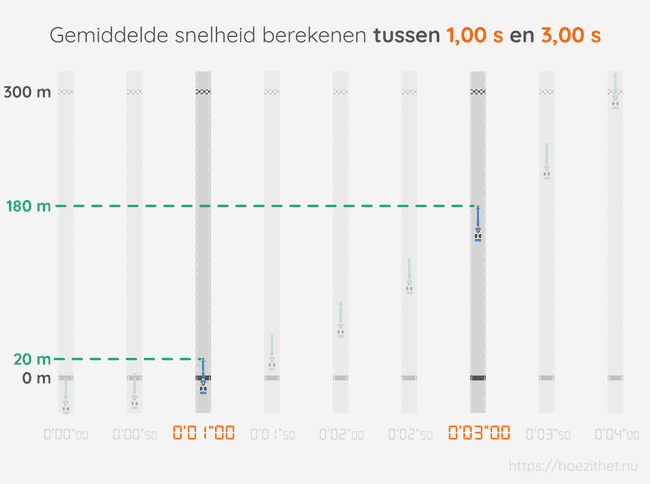
Stel dat we Maria's gemiddelde snelheid willen berekenen tussen $\orange{1{,}00~\si{s}}$ en $\orange{3{,}00~\si{s}}$ .

Daarvoor moeten we de afgelegde afstand (hoeveel (kilo)meter?) delen door de tijd die nodig was (hoeveel uur of seconden?) om die afstand af te leggen:

\begin{aligned} \text{gem. snelheid} &= \frac{\green{\text{afgelegde afstand} }}{\orange{\text{tijd die nodig was}}}\\ \end{aligned}

Wanneer de chronometer op $\orange{1{,}00~\si{s}}$ stond, was Maria $\green{20~\si{m}}$ ver. Bij $\orange{3{,}00~\si{s}}$ , was ze $\green{180~\si{m}}$ ver. De gemiddelde snelheid tussen $\orange{1{,}00~\si{s}}$ en $\orange{3{,}00~\si{s}}$ is dus:

\begin{aligned} \text{gem. snelheid} &= \frac{\green{\text{afgelegde afstand} }}{\orange{\text{tijd die nodig was}}}\\ &= \frac{\green{180~\si{m}} - \green{20~\si{m}}}{\orange{3{,}00~\si{s}} - \orange{1{,}00~\si{s}}}\\ &= \frac{\green{160~\si{m}}}{\orange{2{,}00~\si{s}}}\\ &= 80{,}0~\si{m/s}\\ &= 288~\si{km/h} \end{aligned}

Lekker snel! 🚀

Je ziet dat we voor de afgelegde afstand en de tijd die nodig was telkens een verschil berekenen. Voor de afstand is dat het verschil tussen de tweede positie ( $\green{180~\si{m}}$ ) en de eerste positie ( $\green{20~\si{m}}$ ). Voor de tijd is dat het verschil tussen de tweede tijd ( $\orange{3{,}00~\si{s}}$ ) en de eerste tijd ( $\orange{1{,}00~\si{s}}$ ). Die twee verschillen zetten we vervolgens in een breuk met in de teller (boven) het verschil van posities en in de noemer (onder) het verschil van tijden. We kunnen de formule voor gemiddelde snelheid dus ook als volgt schrijven:

\text{gem. snelheid} = \frac{\green{\text{positie}_2} - \green{\text{positie}_1}}{\orange{\text{tijd}_2} - \orange{\text{tijd}_1}}

Gemiddelde snelheid veralgemenen naar het differentiequotiënt

Stel nu dat we de $\orange{\text{tijd}}$ op de chronometer " $\orange{x}$ " noemen. Maria kan op een bepaald tijdstip $\orange{x}$ natuurlijk maar op één plaats tegelijk zijn. Met elke tijd $\orange{x}$ op de chronometer komt dus hooguit één $\green{\text{positie}}$ overeen. Daarom mogen we zeggen dat Maria's positie een functie is van de tijd.

Als je niet meer goed weet vanaf wanneer een verband tussen twee variabelen (zoals positie en tijd) een functie is, kan je altijd onze les over functies eens nalezen.

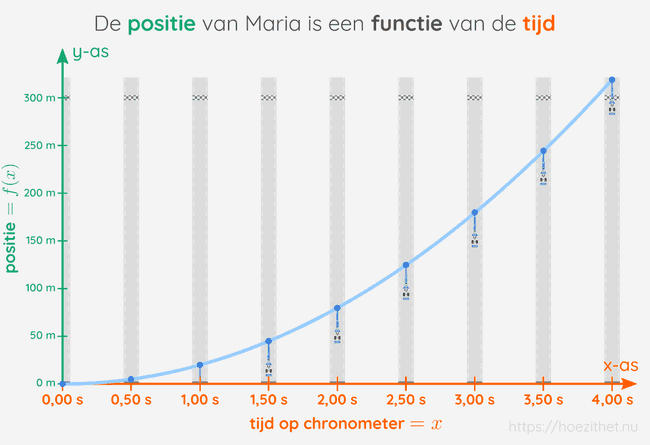
We kunnen de positie die overeenkomt met tijdstip $\orange{x}$ dus de functiewaarde van $\orange{x}$ noemen en afkorten als $\green{f(x)}$ . Wanneer we op de luchtfoto's de racewagens met elkaar verbinden, zien we inderdaad dat de posities mooi de grafiek van een functie volgen waarbij de tijd op de x-as (horizontale as) staat en de positie op de y-as (verticale as):

We kunnen nu onze formule voor gemiddelde snelheid korter schrijven waarbij we

$\green{\text{positie}_2}$ en $\green{\text{positie}_1}$ vervangen door $\green{f(x_2)}$ en $\green{f(x_1)}$
$\orange{\text{tijd}_2}$ en $\orange{\text{tijd}_1}$ vervangen door $\orange{x_2}$ en $\orange{x_1}$

Zo krijgen we:

\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{x_2} - \orange{x_1}}

In de teller (boven) staat $\green{f(x_2)} - \green{f(x_1)}$ . Daarmee berekenen we het verschil van de functiewaarden van $x_2$ en $x_1$ . De teller zegt zo hoeveel de functiewaarde is veranderd tussen $x_1$ en $x_2$ .
In de noemer (onder) staat dan weer het verschil van die $x_2$ en $x_1$ zélf. Door te delen door $\orange{x_2} - \orange{x_1}$ berekenen we de "gemiddelde verandering van de functiewaarde per $x-$ eenheid (bv. per seconde) tussen $x_1$ en $x_2$ " in plaats van gewoon de "verandering van de functiewaarde tussen $x_1$ en $x_2$ ".

Waarom zorgt die deling door

\orange{x_2} - \orange{x_1}

voor een gemiddelde?

Stel dat je de gemiddelde score wilt berekenen die de leerlingen van een bepaalde klas haalden op een test. Dan ga je alle punten optellen en delen door het totaal aantal testen. Door te delen door het totaal aantal testen, krijg je de gemiddelde score per test.

Op dezelfde manier krijgen we de gemiddelde verandering van de functiewaarde per $x-$ eenheid door te delen door $\orange{x_2} - \orange{x_1}$ .

We zeggen dat deze formule de gemiddelde verandering van de functiewaarde berekent per $x-$ eenheid tussen $\orange{x_1}$ en $\orange{x_2}$ .

Toon uitleg

Het is belangrijk om te weten dat we die formule niet enkel kunnen gebruiken om gemiddelde snelheid te berekenen, maar voor nog veel andere soorten van gemiddelde verandering. De formule wordt zelfs zo vaak gebruikt, dat ze een eigen naam heeft gekregen: het differentiequotiënt.

Waar komt de naam differentiequotiënt vandaan?

Nu denk je misschien: "Een differ-watte?! 🤨" Waar komt die naam vandaan? Het woord bestaat uit twee stukken:

differentie-: moeilijk woord voor een aftrekking of verschil, denk maar aan het Engelse woord difference. Dit wijst erop dat er een verschil wordt berekend in de teller en noemer.
-quotiënt: moeilijk woord voor een deling of een breuk. Dit wijst op het feit dat het ene verschil wordt gedeeld door het andere.

Het verschil korter schrijven

Tot slot gaan we het differentiequotiënt nog een tikkeltje korter leren schrijven. Verschillen als " $\green{f(x_2)} - \green{f(x_1)}$ " en " $\orange{x_2} - \orange{x_1}$ " komen namelijk vaak voor en het is lastig om die telkens voluit te moeten schrijven. Daarom gaan we zulke verschillen afkorten. Hiervoor gebruiken we de Griekse hoofdletter $\Delta$ (de delta):

\begin{aligned} \green{f(x_2)} - \green{f(x_1)} &= \green{\Delta f(x)}\\ \orange{x_2} - \orange{x_1} &= \orange{\Delta x} \end{aligned}

Die " $\Delta$ " lijkt wat overweldigend, maar is eigenlijk niets meer dan een verkorte schrijfwijze. Met behulp van deze $\Delta$ , kunnen we het differentiequotiënt als volgt afkorten:

\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{x_2} - \orange{x_1}} = \frac{\green{\Delta f(x)}}{\orange{\Delta x}}

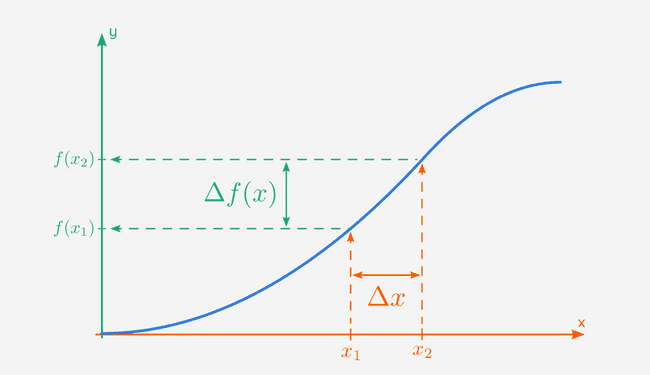
Op een grafiek kan je $\green{\Delta f(x)}$ en $\orange{\Delta x}$ ook aanduiden:

Je zult het waarschijnlijk niet graag horen, maar er is nog een derde en laatste manier om het differentiequotiënt te schrijven. Daarbij gaan we drie dingen veranderen aan de oorspronkelijke formule van het differentiequotiënt:

Vervang $\orange{x_2} - \orange{x_1}$ door $\orange{\Delta x}$ :
$\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{\Delta x}}$
Vervang $x_2$ door $x_1 + \Delta x$ :
$\frac{\green{f(x_1 + \Delta x)} - \green{f(x_1)}}{\orange{\Delta x}}$
Vervang $x_1$ overal door $a$ :
$\frac{\green{f(a + \Delta x)} - \green{f(a)}}{\orange{\Delta x}}$

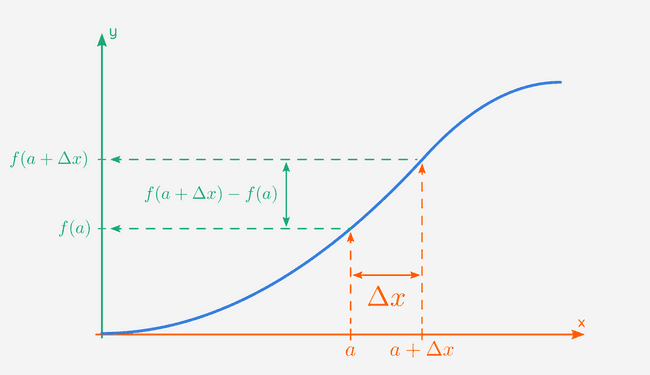
Dat ziet er grafisch zo uit:

We hebben nu drie verschillende manieren gezien om het differentiequotiënt te schrijven:

$\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{x_2} - \orange{x_1}}$
$\frac{\green{\Delta f(x)}}{\orange{\Delta x}}$
$\frac{\green{f(a + \Delta x)} - \green{f(a)}}{\orange{\Delta x}}$

Het is belangrijk om in te zien dat deze alle drie identiek dezelfde berekening maken. De berekening wordt enkel anders verwoord. Kijk dus nog eens extra naar de drie formules voor het differentiequotiënt, bekijk de bijhorende grafieken nogmaals en zorg dat je de gelijkenis begrijpt.

Samengevat

Wat is een differentiequotiënt?

Een differentiequotiënt zegt hoeveel de $\green{\text{functiewaarde}}$ gemiddeld $\orange{\text{per x-eenheid}}$ verandert tussen een gekozen $\orange{x_1}$ en $\orange{x_2}$ .

Het differentiequotiënt is gedefinieerd als:

\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{x_2} - \orange{x_1}}

Door $\green{f(x_2) - f(x_1)}$ te vervangen door $\green{\Delta f(x)}$ en $\orange{x_2 - x_1}$ door $\orange{\Delta x}$ , kunnen we het differentiequotiënt ook schrijven als:

\frac{\green{\Delta f(x)}}{\orange{\Delta x}}

Een andere schrijfwijze vervangt $\orange{x_2} - \orange{x_1}$ door $\orange{\Delta x}$ , $\green{f(x_2)}$ door $\green{f(x_1 + \Delta x)}$ en vervangt ten slotte $\green{x_1}$ overal door $\green{a}$ :