Domein en beeld

Inhoud

Domein van een functie
Beeld van een functie
Domein en beeld op een grafiek
Samengevat

We kunnen niet altijd eender welk getal als $x$ kiezen om in ons functievoorschrift te stoppen. Omgekeerd is het mogelijk dat niet eender welk getal als $y$ uit de functie komt. Deze twee eigenschappen van een functie worden beschreven door het domein en het beeld van de functie.

Domein van een functie

Het domein van een functie is de verzameling van x-waarden waarvoor er een functiewaarde (een y-waarde) bestaat.

Voor elke x-waarde die niet in het domein zit, bestaat er géén y-waarde.
Voor elke x-waarde die wel in het domein zit, bestaat er juist één y-waarde.

Een typisch voorbeeld is het domein van de functie die als functievoorschrift heeft

f(x) = \sqrt{x}

Omdat de wortel van een negatief getal niet bestaat, kan $f(x)$ niet bestaan wanner x negatief is. Er bestaan met andere woorden géén y-waarden voor negatieve x-waarden. Het domein van deze functie $f$ is dus alle positieve reële getallen, want enkel voor positieve x-waarden bestaat er een functiewaarde. We schrijven:

\mathrm{dom}~f = \mathbb{R}^+

Dit kunnen we ook schrijven als een interval:

\mathrm{dom}~f = [0; +\infty[%]

Beeld van een functie

Het beeld of het bereik van een functie is de verzameling van alle y-waarden die ooit uit de functie kunnen komen.

Een typisch voorbeeld is het beeld van de functie die als functievoorschrift heeft

f(x) = x^2

Omdat het kwadraat van elk reëel getal positief is, kunnen er uit deze functie $f$ enkel positieve getallen komen. Met andere woorden is het beeld van deze functie alle positieve reële getallen. We schrijven:

\mathrm{bld}~f = \mathbb{R}^+

Dit kunnen we natuurlijk ook schrijven als een interval:

\mathrm{bld}~f = [0; +\infty[%]

Domein en beeld op een grafiek

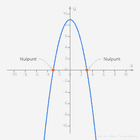
Het domein en beeld van een functie kan je ook aflezen van de grafiek van die functie. Neem bijvoorbeeld de grafiek van de functie

f(x) = 3\cdot \sqrt{x + 5} - 6

Die grafiek ziet er zo uit:

Om op deze grafiek het domein af te lezen, moet je de grafiek projecteren op de x-as. Het resultaat van de projectie is aangeduid in het groen op de x-as. We gaan ervan uit dat de grafiek oneindig blijft verder stijgen aan de rechterkant. We zien dan dat $\green{\mathrm{dom}~f = [-5; +\infty[}$ .

Het beeld (of het bereik) van diezelfde functie kunnen we vinden door de grafiek nu te projecteren op de y-as. Op de onderstaande grafiek zie je het resultaat van deze projectie in het groen op de y-as.