Grafieken van functies

Inhoud

Veel puntjes vormen een curve
Hoogstens één y voor elke x

Stel dat we een functie hebben met het volgende functievoorschrift:

f(x) = -\frac{1}{2}x^2 + 4x - 6

We kunnen dan verschillende x-waarden invullen in dit voorschrift om te kijken welke y-waarde erbij hoort. We kunnen bijvoorbeeld de x-waarden $0$ , $1$ , $2$ , enz. tot en met $10$ eens in het functievoorschrift stoppen en telkens de functiewaarde uitrekenen. Zo krijgen we de volgende waardentabel:

$\orange{x}$	$\green{y}$ of de functiewaarde van $\orange{x}$
$\orange{0}$	$\green{-6}$
$\orange{1}$	$\green{-2{,}5}$
$\orange{2}$	$\green{0}$
$\orange{3}$	$\green{1{,}5}$
$\orange{4}$	$\green{2}$
$\orange{5}$	$\green{1{,}5}$
$\orange{6}$	$\green{0}$
$\orange{7}$	$\green{-2.5}$
$\orange{8}$	$\green{-6}$
$\orange{9}$	$\green{-10.5}$
$\orange{10}$	$\green{-16}$

In elke rij van onze waardentabel staat een x-waarde en een bijhorende functiewaarde of y-waarde. Elke rij in onze waardentabel kunnen we dus zien als een puntje met een x- en een y-coördinaat. Voor de x-waarde $\orange{x = 4}$ , bijvoorbeeld, hadden we $\green{y = 2}$ gevonden. We kunnen deze x- en y-waarde dan voorstellen door een puntje met coördinaten $(\orange{4};~\green{2})$ . In een assenstelsel ziet dat puntje er zo uit:

Zo kunnen we alle puntjes die in onze waardentabel staan gaan voorstellen als puntjes in een assenstelsel:

Veel puntjes vormen een curve

In ons vorige voorbeeld hadden we maar van elf verschillende x-waarden de y-waarde gezocht. We kunnen eens kijken wat er gebeurt als we van veel meer x-waarden de y-waarde gaan zoeken. Bijvoorbeeld voor de x-waarden $0$ , $0{,}1$ , $0{,}2$ , $0{,}3$ enz. helemaal tot $10$ . De waardentabel die we dan krijgen is veel groter dan de vorige. Omdat er zoveel rijen in staan, tonen we hieronder maar een klein stukje ervan:

$\orange{x}$	$\green{y}$ of de functiewaarde van $\orange{x}$
$\orange{0{,}0}$	$\green{-6}$
$\orange{0{,}1}$	$\green{-5{,}605}$
$\orange{0{,}2}$	$\green{-5{,}22}$
$\orange{0{,}3}$	$\green{-4{,}845}$
$\orange{0{,}4}$	$\green{-4{,}48}$
$\orange{0{,}5}$	$\green{-4{,}125}$
$\orange{0{,}6}$	$\green{-3{,}78}$
$\orange{0{,}7}$	$\green{-3{,}445}$
$\orange{0{,}8}$	$\green{-3{,}12}$
$\orange{0{,}9}$	$\green{-2{,}805}$
$\orange{1{,}0}$	$\green{-2{,}5}$
$\orange{1{,}1}$	$\green{-2{,}205}$
...	...
$\orange{8{,}9}$	$\green{-10{,}005}$
$\orange{9{,}0}$	$\green{-10{,}5}$
$\orange{9{,}1}$	$\green{-11{,}005}$
$\orange{9{,}2}$	$\green{-11{,}52}$
$\orange{9{,}3}$	$\green{-12{,}05}$
$\orange{9{,}4}$	$\green{-12{,}58}$
$\orange{9{,}5}$	$\green{-13{,}125}$
$\orange{9{,}6}$	$\green{-13{,}68}$
$\orange{9{,}7}$	$\green{-14{,}245}$
$\orange{9{,}8}$	$\green{-14{,}82}$
$\orange{9{,}9}$	$\green{-15{,}405}$
$\orange{10{,}0}$	$\green{-16}$

Als we voor al deze rijen een puntje zetten bij de bijhorende x- en y-coördinaat, dan krijgen we deze mooie figuur:

Als we nu nog meer x-waarden zouden kiezen, bijvoorbeeld $0$ , $0{,}01$ , $0{,}02$ , $0{,}03$ enz. helemaal tot $10$ , daarvoor ook weer alle y-waarden zouden uitrekenen en op een assenstelsel zouden tonen, dan krijgen we deze figuur:

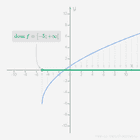
We hebben nu zoveel puntjes op ons assenstelsel dat we bijna niet meer zien dat het aparte puntjes zijn. We zien het als één doorlopende curve. Deze curve noemen we de grafiek van de functie.

Hoogstens één $y$ voor elke $x$

We weten dat er bij een functie voor een bepaalde waarde van $x$ hoogstens één waarde van $y$ bestaat. Grafisch betekent dit dat er op de curve van een functie nooit twee punten boven elkaar liggen. De curve hieronder is een voorbeeld van een curve waar er voor bepaalde waarden van $x$ meerdere waarden van $y$ bestaan. Met andere woorden is hier $y$ geen functie van $x$ . Zonder het onderste stukje dat lijkt "terug te keren" is $y$ wel een functie van $x$ .