Benaderingsregels

Inhoud

Afronden na de komma
Afronden vóór de komma
Optellingen en aftrekkingen
Vermenigvuldigingen en delingen
Enkel toepassen bij meetresulaten
Samengevat

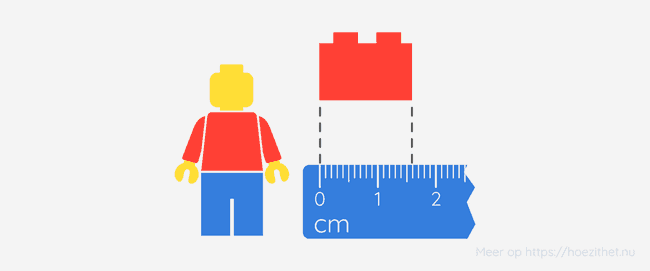
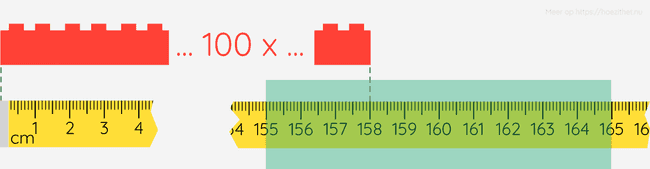
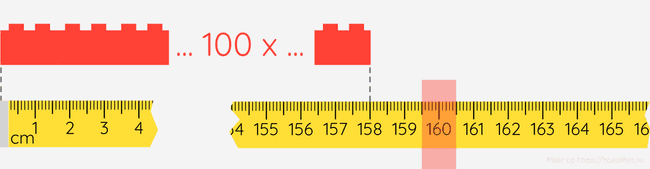
Als we berekeningen doen met metingen, moeten we altijd in ons achterhoofd houden dat metingen nooit exact zijn. Stel dat we bijvoorbeeld een meetlat naast een LEGO-blokje leggen, en we meten dat de zijde $1{,}6 \si{ cm}$ is.

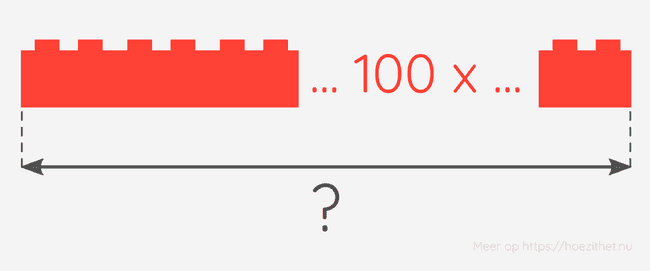
Als we 100 zulke blokjes naast elkaar leggen, hoe lang zal die rij blokjes dan zijn?

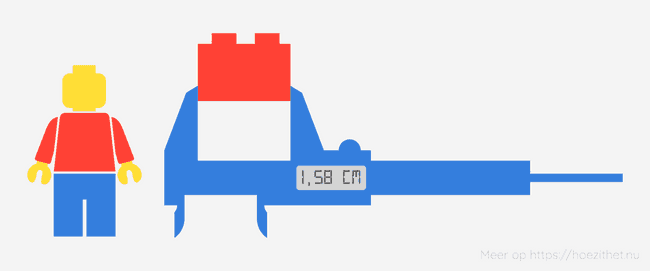
Dat lijkt heel eenvoudig, gewoon $100 \cdot 1{,}6 \si{ cm} = 160 \si{ cm}$ . We hebben het blokje echter gemeten met een meetlat die maar tot op $0{,}1 \si{ cm}$ nauwkeurig kan meten. Stel dat we het blokje nu meten met een schuifmaat die tot op $0{,}01 \si{ cm}$ nauwkeurig kan meten. Nu vinden we dat het blokje $1{,}58 \si{ cm}$ is.

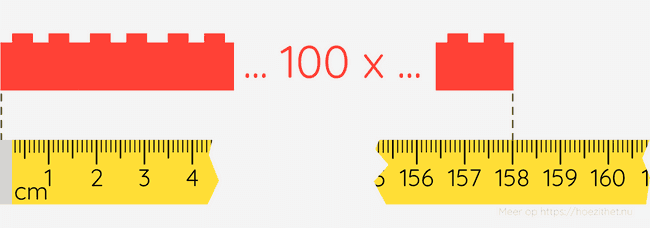
Als we 100 blokjes naast elkaar zouden leggen, zullen we dus een rij van $158 \si{ cm}$ krijgen, niet $160 \si{ cm}$ .

Met benaderingsregels kunnen we de onzekerheid van een berekening uitdrukken. Als we de benaderingsregels toepassen die we straks zullen leren, krijgen we $1{,}6 \si{ m}$ voor de eerste berekening en $1{,}58 \si{ m}$ voor de tweede berekening. Het belangrijke hierbij is dat er $1{,}6$ staat en niet $1{,}6\red{0}$ .

Met $1{,}6 \si{ m}$ bedoelen we namelijk: "Iets tussen $1{,}55 \si{ m}$ en $1{,}65 \si{ m}$ ," en inderdaad, $1{,}58 \si{ m}$ ligt binnen die foutenmarge.

Als we bij de eerste berekening $1{,}6\red{0}$ hadden geschreven, zou dat betekenen: "Iets tussen $1{,}5\red{95} \si{ m}$ en $1{,}6\red{05} \si{ m}$ ," maar dat is fout, want $1{,}58 \si{ m}$ ligt buiten die foutenmarge.

Door na onze berekeningen benaderingsregels toe te passen, zorgen we dat de uitkomst de juiste foutenmarge heeft.

Afronden na de komma

Voor we de benaderingsregels uit de doeken doen, frissen we nog snel even op hoe je getallen moet afronden.

Rond af naar boven als het volgende cijfer groter of gelijk aan 5 is;
Rond af naar beneden als het volgende cijfer kleiner dan 5 is.

Als voorbeeld ronden we $384{,}9503$ af tot een bepaald aantal cijfers na de komma.

Voor afronding	Soort afronding	Na afronding	Uitleg
$384{,}\orange{9}\gold{5}03$	Op de tienden	$385{,}\orange{0}$	$\gold{5} \ge 5$ dus $\orange{9}$ wordt $1\orange{0}$ , waardoor de $4$ een $5$ wordt
$384{,}9\orange{5}\gold{0}3$	Op de honderdsten	$384{,}9\orange{5}$	$\gold{0} \lt 5$ dus $\orange{5}$ blijft $\orange{5}$
$384{,}95\orange{0}\gold{3}$	Op de duizendsten	$384{,}95\orange{0}$	$\gold{3} \lt 5$ dus $\orange{0}$ blijft $\orange{0}$

Afronden vóór de komma

Soms moeten we ook vóór de komma afronden. Dat kunnen we met behulp van machten van 10. We zullen weer $384{,}9503$ gebruiken als voorbeeld.

Voor afronding	Soort afronding	Na afronding	Uitleg
$38\orange{4}{,}\gold{9}503$	Op de eenheden	$38\orange{5}\cdot 10^0$ of gewoon $38\orange{5}$	$\gold{9} \ge 5$ dus $\orange{4}$ wordt $\orange{5}$ Vermenigvuldigen met $10^0 = 1$ omdat we afronden op de eenheden
$3\orange{8}\gold{4}{,}9503$	Op de tientallen	$3\orange{8}\cdot 10^1$	$\gold{4} \lt 5$ dus $\orange{8}$ blijft $\orange{8}$ Vermenigvuldigen met $10^1 = 10$ omdat we afronden op de tientallen
$\orange{3}\gold{8}4{,}9503$	Op de honderdtallen	$\orange{4}\cdot 10^2$	$\gold{8} \ge 5$ dus $\orange{3}$ wordt $\orange{4}$ Vermenigvuldigen met $10^2 = 100$ omdat we afronden op de honderdtallen

Optellingen en aftrekkingen

Nadat we berekeningen hebben gedaan, zullen we bijna altijd de benaderingsregels moeten toepassen. Welke regels we moeten toepassen, hangt af van de bewerkingen die we hebben gedaan tijdens de berekening.

Voor optellingen en aftrekkingen kijken we naar het aantal cijfers na de komma. We moeten de uitkomst afronden zodat die hetzelfde aantal cijfers na de komma heeft als het getal in de berekening met het minst aantal cijfers na de komma.

Neem bijvoorbeeld de volgende berekening met drie gemeten afstanden:

24{,}28~\si{m} + 9{,}1~\si{m} - 3{,}35~\si{m}

Deze berekening heeft drie termen:

Term	Aantal cijfers na de komma
$24{,}\orange{28}~\si{m}$	2
$9{,}\orange{1}~\si{m}$	1
$-3{,}\orange{35}~\si{m}$	2

Het kleinste aantal cijfers na de komma is dus 1. Dat betekent dat we de uitkomst moeten afronden tot op 1 cijfer na de komma (afronden op de tienden dus). De uitkomst van de berekening zelf is:

24{,}28~\si{m} + 9{,}1~\si{m} - 3{,}33~\si{m} = 36{,}75~\si{m}

Als we dit vervolgens afronden op de tienden, krijgen we:

36{,}\orange{7}\gold{5}~\si{m} \approx 36{,}\orange{8}~\si{m}

Vermenigvuldigingen en delingen

Voor vermenigvuldigingen en delingen kijken we naar het aantal buidende cijfers. We moeten de uitkomst afronden zodat die hetzelfde aantal beduidende cijfers heeft als het getal in de berekening met het minst aantal beduidende cijfers.

Stel bijvoorbeeld dat je de volgende berekening moet maken:

0{,}247~\si{cm} \cdot 3{,}42~\si{cm} \cdot 9{,}1~\si{cm}

Deze berekening heeft drie factoren:

Factor	Aantal beduidende cijfers
$0{,}\orange{247}~\si{cm}$	3
$\orange{3}{,}\orange{42}~\si{cm}$	3
$\orange{9}{,}\orange{1}~\si{cm}$	2

Het kleinste aantal beduidende cijfers is dus 2. Dat betekent dat we de uitkomst moeten afronden tot 2 beduidende cijfers. De uitkomst is:

0{,}247 \cdot 3{,}42 \cdot 9{,}1 = 7{,}687134

Deze uitkomst moeten we afronden zodat enkel de eerste 2 beduidende cijfers overblijven ( $7$ en $6$ ). We moeten dus afronden op de tienden (1 plaats na de komma):

7{,}\orange{6}\gold{8}7134 \approx 7{,}\orange{7}

Enkel toepassen bij meetresulaten

We gebruiken de benaderingsregels om rekening te houden met de nauwkeurigheid van een meting. We moeten de benaderingsregels daarom enkel toepassen op getallen die een meetresultaat voorstellen.

Stel bijvoorbeeld dat we de omtrek van een cirkel met straal $r = 5{,}3~\si{cm}$ moeten berekenen. Dat kan met de volgende formule:

\text{Omtrek} = 2\pi r

Ingevuld:

\text{Omtrek} = 2\pi \cdot 5{,}3~\si{cm}

De $2$ in de bovenstaande berekening is geen meetresultaat, maar is deel van de formule om de omtrek van een cirkel te berekenen. Dat getal telt dus niet mee voor de benaderingsregels. Hetzelfde geldt voor $\pi$ . Enkel $5{,}3~\si{cm}$ is een meting. De uitkomst moet dus evenveel beduidende cijfers hebben als $5{,}3~\si{cm}$ , namelijk twee beduidende cijfers:

\begin{aligned} \text{Omtrek} &= 2\pi \cdot 5{,}3~\si{cm}\\ &= 2\pi \cdot 5{,}3~\si{cm}\\ &= 33{,}30088\ldots~\si{cm}\\ &\breq 33~\si{cm}\\ \end{aligned}

Samengevat

Benaderingsregels

De uitkomst van een optelling of aftrekking moet hetzelfde aantal cijfers na de komma hebben als het getal in de berekening met het kleinste aantal cijfers na de komma;
De uitkomst van een vermenigvuldiging of deling moet hetzelfde aantal beduidende cijfers hebben als het getal in de berekening met het kleinste aantal beduidende cijfers.

Download deze les als pdf