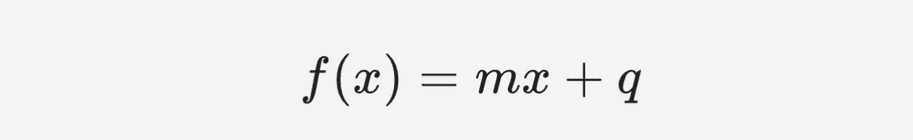Het tekenschema van een eerstegraadsfunctie

Inhoud

Stappenplan om tekenschema van eerstegraadsfunctie op te stellen
Samengevat

Het tekenschema of tekenverloop van een functie vertelt ons voor welke x-waarden de functie positief, negatief of nul is.

We beginnen met een voorbeeld. Stel dat de volgende eerstegraadsfunctie gegeven is:

f(x) = -3x + 12

Voor deze functie zullen x-waarden kleiner dan $4$ een positieve functiewaarde geven (hoe we aan die $4$ komen, leggen we later uit):

\begin{aligned} f({\orange{3{,}99}}) &= -3\cdot {\orange{3{,}99}} + 12\\ &= 0{,}03\\ &\gt 0 \end{aligned}

x = {\orange{3{,}99}}

Verschuif de bovenstaande slider naar links. Je ziet dat voor alle x-waarden kleiner dan $4$ de functiewaarde positief is.

Wanneer we x-waarden groter dan $4$ invullen, krijgen we daarentegen negatieve functiewaarden (verschuif de onderstaande slider naar rechts):

\begin{aligned} f({\orange{4{,}01}}) &= -3\cdot {\orange{4{,}01}} + 12\\ &= -0{,}03\\ &\lt 0 \end{aligned}

x = {\orange{4{,}01}}

Wanneer $x = \orange{4}$ , krijgen we dan weer een functiewaarde gelijk aan nul:

\begin{aligned} f(4) &= -3\cdot \orange{4} + 12\\ &= 0 \end{aligned}

Samengevat:

Als $x < \orange{4}$ , dan is $f(x) \green{> 0}$
Als $x = \orange{4}$ , dan is $f(x) = 0$
Als $x > \orange{4}$ , dan is $f(x) \red{< 0}$

Dit zetten we als volgt in een tekenschema:

$x$	$-\infty$		$\htmlId{null}{\orange{4}}$		$+\infty$
$f(x)$		$\htmlId{null}{\green{+}}$	$0$	$\htmlId{null}{\red{-}}$

Het tekenschema toont dat wanneer $x$ tussen $-\infty$ en $4$ ligt (en dus kleiner is dan $4$ ), dat $f(x)$ dan positief is ( $\green{+}$ ). Wanneer $x$ gelijk is aan $4$ , zien we in het tekenschema dat $f(x)$ gelijk is aan $0$ . Wanneer $x$ ten slotte tussen $4$ en $+\infty$ ligt, toont het tekenschema dat $f(x)$ negatief is ( $\red{-}$ ).

Maar waar komt die $4$ juist vandaan? En hoe kunnen we zo'n tekenschema gaan maken voor andere eerstegraadsfuncties? Dit leggen we uit in de volgende paragraaf.

Stappenplan om tekenschema van eerstegraadsfunctie op te stellen

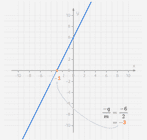
We weten dat de grafiek van een eerstegraadsfunctie een rechte is. Die rechte snijdt de x-as exact één keer. Dit snijpunt is het nulpunt van de functie. Hieronder zie je bijvoorbeeld de grafiek van $f(x) = -3x + 12$ met het nulpunt aangeduid.

Omdat de rico ( $m$ ) van de functie kleiner is dan nul, daalt de grafiek. We zien dat de grafiek vòòr het nulpunt boven de x-as liggen en na het nulpunt onder de x-as. Vòòr het nulpunt hebben we dus positieve functiewaarden en na het nulpunt hebben we negatieve functiewaarden.

In de onderstaande interactieve illustratie kan je zelf de waarde van $m$ veranderen naar andere negatieve waarden om zo de grafiek en het tekenschema van andere functies te verkrijgen. Je ziet dat voor eender welke negatieve waarde van $m$ , de functie altijd van positief naar negatief gaat. Merk ook op dat de waarde van $q$ hier geen invloed op heeft.

$x$	$-\infty$		$\htmlId{hzhR5ial6qH5hzh}{\orange{4}}$		$+\infty$
$f(x)$		$\htmlId{hzhR5ial6qH3hzh}{\green{+}}$	$0$	$\htmlId{hzhR5ial6qH2hzh}{\red{-}}$

m = -3

q = 12

Wanneer $m$ groter is dan nul, dan zal de grafiek van de functie stijgen en dan zal de grafiek vòòr het nulpunt onder de x-as liggen en na het nulpunt boven de x-as. Vòòr het nulpunt hebben we dus negatieve functiewaarden en na het nulpunt hebben we positieve functiewaarden.

We zien in de onderstaande illustratie inderdaad dat voor eender welke positieve waarde van $m$ , de functie altijd van negatief naar positief gaat.

$x$	$-\infty$		$\htmlId{hzhR6aal6qH5hzh}{\orange{-1}}$		$+\infty$
$f(x)$		$\htmlId{hzhR6aal6qH2hzh}{\red{-}}$	$0$	$\htmlId{hzhR6aal6qH3hzh}{\green{+}}$

m = 1

q = 1

In het algemeen zien we dus het volgende:

De punten vòòr het nulpunt hebben y-coördinaten met het tegengestelde teken van $m$ .
Het nulpunt zelf heeft een y-coördinaat gelijk aan $0$ .
De punten na het nulpunt hebben y-coördinaten met hetzelfde teken als $m$ .

In de volgende illustratie kan je zowel positieve als negatieve waarden voor $m$ kiezen. Verander de waarde van $m$ en ga op die manier zelf na dat de bovenstaande vaststellingen kloppen.

$x$	$-\infty$		$\htmlId{hzhR7aal6qH5hzh}{\orange{-1}}$		$+\infty$
$f(x)$		$\htmlId{hzhR7aal6qH2hzh}{\red{-}}$	$0$	$\htmlId{hzhR7aal6qH3hzh}{\green{+}}$

m = 1

q = 1

Deze vaststellingen kunnen we gebruiken om een stappenplan te maken voor het opstellen van het tekenschema van eender welke eerstegraadsfunctie. Herinner je hierbij dat de x-coördinaat van het nulpunt van een eerstegraadsfunctie altijd gelijk is aan $\frac{-q}{m}$ . Vòòr en na het nulpunt is dus hetzelfde als vòòr en na x-waarde $\frac{-q}{m}$ .

💡 Het tekenschema van een eerstegraadsfunctie opstellen

Om het tekenschema van een eerstegraadsfunctie met voorschrift $f(x) = mx + q$ op te stellen, doen we het volgende:

Bereken de nulwaarde van de eerstegraadsfunctie: $\frac{-q}{m}$ , en plaats ze in het tekenschema in de rij van de x-waarden. In de rij van $f(x)$ zet je daar een $0$ .
Tussen x-waarden $-\infty$ en $\frac{-q}{m}$ zet je in de rij van $f(x)$ het tegengestelde teken van $m$ .
Tussen x-waarden $\frac{-q}{m}$ en $+\infty$ zet je in de rij van $f(x)$ hetzelfde teken als $m$ .

$x$	$-\infty$		$\frac{-q}{m}$		$+\infty$
$f(x)$		$\text{Tegengesteld}\\\text{teken van }m$	$0$	$\text{Zelfde teken}\\\text{als }m$

Oefening NaN

Wat is het tekenschema van de functie

f(x) = 6\cdot x-6

(Noteer je antwoord zelf op papier.)

Samengevat

💡 Het tekenschema van een eerstegraadsfunctie opstellen

Om het tekenschema van een eerstegraadsfunctie met voorschrift $f(x) = mx + q$ op te stellen, doen we het volgende:

Bereken de nulwaarde van de eerstegraadsfunctie: $\frac{-q}{m}$ , en plaats ze in het tekenschema in de rij van de x-waarden. In de rij van $f(x)$ zet je daar een $0$ .
Tussen x-waarden $-\infty$ en $\frac{-q}{m}$ zet je in de rij van $f(x)$ het tegengestelde teken van $m$ .
Tussen x-waarden $\frac{-q}{m}$ en $+\infty$ zet je in de rij van $f(x)$ hetzelfde teken als $m$ .