Afleidbaarheid van een functie

We hebben al geleerd hoe we de ogenblikkelijke verandering, of de afgeleide, in een punt $x = a$ kunnen berekenen:

We hebben ons echter nooit afgevraagd of die afgeleide wel altijd berekend kan worden. In deze les leren we over de afleidbaarheid van een functie. We gaan zien dat sommige (meestal vrij exotische) functies niet voor elke keuze van $x = a$ kunnen afgeleid worden.

Linker- en rechterlimiet, wat was dat weer?

Voor we over afleidbaarheid van een functie beginnen, moeten we eerst weten wat een linker- en rechterlimiet weer zijn. De limiet in onze formule voor het berekenen van de afgeleide van $f(x)$ in $x = a$ laat $\Delta x$ naar $0$ gaan:

Er zijn echter twee manieren om $\Delta x$ naar $0$ te laten gaan:

• We kunnen $\Delta x$ kleiner houden dan $0$ en dichter en dichter naar $0$ laten gaan
• Of we kunnen $\Delta x$ groter houden dan $0$ en dichter en dichter naar $0$ laten gaan.

We zien dat in zowel de linker- als rechterkolom de getallen steeds dichter en dichter bij $0$ komen.

• Wanneer we $\Delta x$ kleiner houden dan $0$, zeggen we dat we de linkerlimiet berekenen (omdat we van links naar $0$ gaan). Dit schrijven we als
  $$\lim_{\Delta x \lt{\to} 0}$$
  Let op het kleiner dan-teken ($\lt$) onder de pijl van de limiet.
• Wanneer we $\Delta x$ groter houden dan $0$, zeggen we dat we de rechterlimiet berekenen (omdat we van rechts naar $0$ gaan). Dit schrijven we als
  $$\lim_{\Delta x \gt{\to} 0}$$
  Let op het groter dan-teken ($\gt$) onder de pijl van de limiet.

In veel gevallen zal je voor de linker- en rechterlimiet hetzelfde vinden. Wanneer de linker- en rechterlimiet aan elkaar gelijk zijn, zeggen we dat de limiet zelf bestaat.

Linker- en rechterafgeleide

Net als de linker- en rechterlimiet, is er ook een linker- en rechterafgeleide:

• De linkerafgeleide in $x = a$ is de afgeleide die je krijgt door de linkerlimiet te berekenen:

  $$\gray{\orange{\lim_{\Delta x \lt{\to} 0}} \frac{ f(a + \Delta x) - f(a) }{\Delta x}}$$

• De rechterafgeleide in $x = a$ is de afgeleide die je krijgt door de rechterlimiet te berekenen:

  $$\gray{\orange{\lim_{\Delta x \gt{\to} 0}} \frac{ f(a + \Delta x) - f(a) }{\Delta x}}$$

Of de linker- en/of rechterafgeleide bestaat en of ze gelijk zijn aan elkaar, bepaalt de afleidbaarheid van de functie in $x = a$. Er zijn drie gevallen:

• Wanneer de linkerafgeleide bestaat, zeggen we dat de functie links afleidbaar is in $x = a$.
• Wanneer de rechterafgeleide bestaat, zeggen we dat de functie rechts afleidbaar is in $x = a$.
• Wanneer de linker- en rechterafgeleide van $f(x)$ in $x = a$ allebei bestaan en gelijk zijn aan elkaar, zeggen we dat $f(x)$ afleidbaar is in $x = a$.

Linker- en rechterafgeleide in functie met gaten

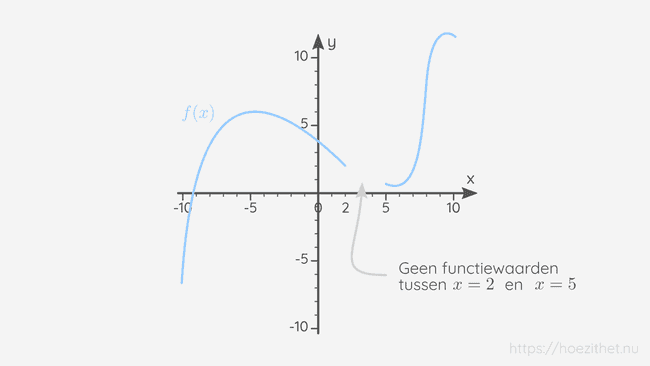
Een typisch voorbeeld van een functie die niet overal afleidbaar is, is een functie waar gaten in zitten. Zo'n functie noemen we een discontinue functie. We zien in onderstaande functie dat er een gat zit tussen $x = 2$ en $x = 5$. Dat gat zorgt ervoor dat we in $x = 2$ geen rechterlimiet kunnen berekenen, omdat wanneer $\Delta x$ iets groter is dan $0$, dan moeten we de functiewaarde berekenen van een x-waarde die iets groter is dan $2$. Maar alle x-waarden die iets groter zijn dan $2$ (bv. $2{,}1$; $2{,}01$; $2{,}001$;...) liggen in die opening en hebben dus geen functiewaarden.

De functie is dus enkel links afleidbaar en niet rechts afleidbaar in $x = 2$. Op dezelfde manier kan je erachter komen dat diezelfde functie enkel rechts afleidbaar is in $x = 5$ en niet links afleidbaar. In $x = 6$ is de functie dan weer zowel rechts als links afleidbaar én zijn deze afgeleiden aan elkaar gelijk. In $x = 6$ is de functie dus afleidbaar.

Alle punten die tussen $x = 2$ en $x = 5$ liggen hebben geen functiewaarde. Daarvoor kunnen we dus noch de linker- noch de rechterafgeleide berekenen. In die punten is de functie uiteraard ook niet afleidbaar.

Een functie die overal afleidbaar is, is altijd continu

Als we met gaten in een functie zitten, krijgen we dus altijd aan de grenzen van die opening een punt dat niet afleidbaar is omdat ofwel de linker- ofwel de rechterafgeleide niet bestaat. In de opening zelf is er geen enkel punt afleidbaar omdat noch de linker- noch de rechterafgeleide bestaat.

Wanneer een functie in elk punt van haar domein afleidbaar is, is het dus onmogelijk dat die functie discontinu is. We kunnen dus stellen dat een functie die overal afleidbaar is, altijd continu is (geen gaten bevat).

Functies met "knikken" zijn niet afleidbaar in de knik

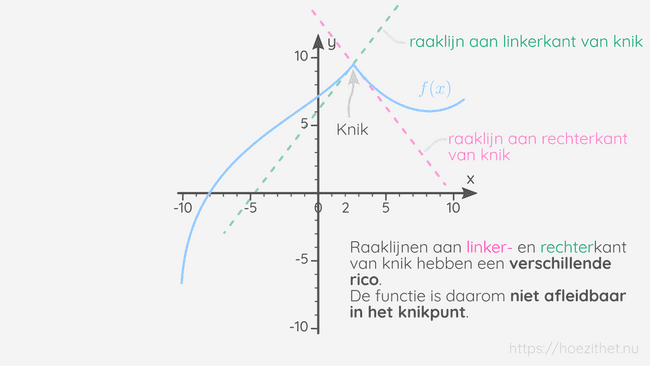
Een ander typisch voorbeeld van een functie die niet overal afleidbaar is, is een functie met een "knik". Die functies zijn niet afleidbaar in de "knik" zelf. Dit kan je eenvoudig begrijpen door een raaklijn aan de linker- en rechterkant van de knik te tekenen. Je ziet dat deze raaklijnen een verschillende richtingscoëfficiënt hebben. De linker- en rechterafgeleide in het knikpunt zijn dus niet gelijk aan elkaar en daarom is de functie in dat punt niet afleidbaar.

Functies met verticale raaklijnen zijn niet afleidbaar bij die raaklijn

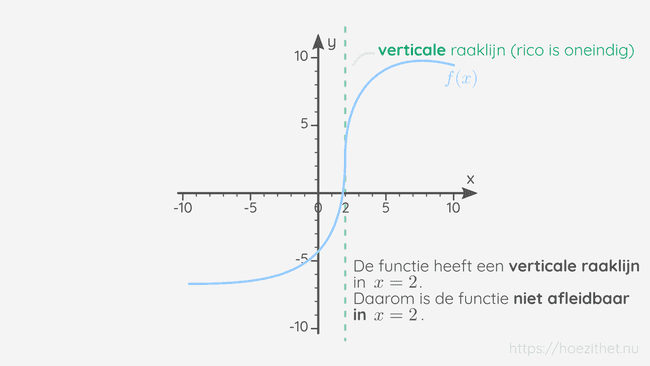
Ten slotte zorgen verticale raaklijnen ook voor niet-afleidbare punten van een functie. Dat komt omdat een verticale raaklijn een oneindig grote rico heeft. De linker- en rechterafgeleiden zijn dus gelijk aan $+\infty$ of $-\infty$ en zijn daarom geen elementen van $\mathbb{R}$.

Merk op dat een verticale asymptoot ook zorgt voor een verticale raaklijn aan de grafiek van de functie. Een functie met een verticale asymptoot is dus niet afleidbaar op de x-waarde waar de asymptoot zich bevindt.

Samengevat

Hoe duidelijk vond je deze les?

Niet duidelijk

Redelijk duidelijk

Heel duidelijk

👈 Vorige les: De afgeleide als rico van een raaklijn

Volgende les: De afgeleide van een functie 👉

Vragen en reacties