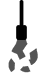De afgeleide als rico van een raaklijn

Inhoud

Wat was dat weer, een rico?
Hoe berekenen we die rico weer?
Het differentiequotiënt is ook een rico
De limiet zorgt voor een raaklijn
De afgeleide is de rico van de raaklijn in x = a
Samengevat

We hebben al geleerd hoe we de ogenblikkelijke verandering, of de afgeleide, van een functie $f(x)$ in een punt $x = a$ kunnen berekenen:

f'(a) = \lim_{\Delta x \to 0} \frac{ \green{f(a + \Delta x)} - \green{f(a)} }{\orange{\Delta x}}

Komt deze formule wat uit de lucht gevallen voor jou? 🤨 Lees dan zeker onze les over het berekenen van de afgeleide in een punt en onze les over het differentiequotiënt eens na.

In deze les gaan we leren dat deze formule eigenlijk ook de formule is voor het berekenen van de richtingscoëfficiënt van de raaklijn aan de grafiek van de functie $f(x)$ voor $x = a$ . Wat een mond vol! 🤯 Maar geen paniek, we leggen het je stap voor stap uit!

Wat was dat weer, een rico?

De richtingscoëfficiënt (afgekort "rico") van een eerstegraadsfunctie is een maat voor hoe steil de rechte is (herinner je dat een eerstegraadsfunctie altijd een rechte is). Je kan de rico van een eerstegraadsfunctie als volgt uit de grafiek van de functie halen:

Ga ergens op de rechte staan, maakt niet uit waar
Schuif één stapje (een eenheid) op in de x-richting
Kijk hoeveel de rechte is gedaald of gestegen. Als de rechte is gedaald, is de rico negatief. Als de rechte is gestegen, is de rico positief.

Hoe berekenen we die rico weer?

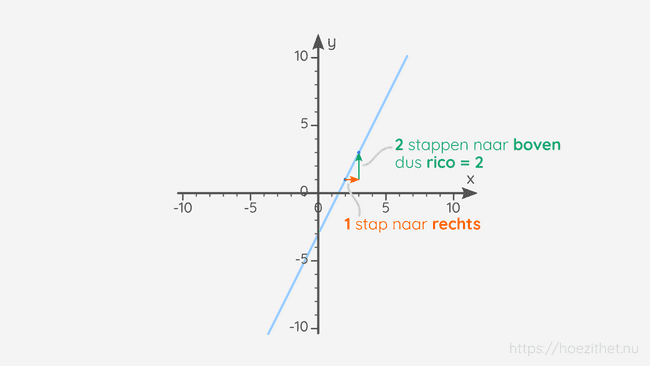
De rico is dus hoeveel een eerstegraadsfunctie stijgt of daalt wanneer je één x-eenheid opschuift naar rechts. Stel dat we eens stoer willen doen, en we schuiven twee eenheden op naar rechts of zelfs drie eenheden 😎 en kijken hoeveel we gestegen of gedaald zijn. Die getallen gaan natuurlijk niet meer gelijk zijn aan onze rico. Maar zie je een verband met de rico?

Je ziet dat als we twee eenheden opschuiven, we ook met twee keer de rico zullen stijgen of dalen. En als we drie eenheden opschuiven, zullen we ook met drie keer de rico stijgen of dalen. Als we hoeveel we stijgen of dalen dus gaan delen door het aantal stappen opzij, dan krijgen we altijd de rico! 💡

\text{rico} = \frac{\green{\text{hoeveel we stijgen of dalen}}}{\orange{\text{aantal stappen opzij}}}

Het aantal stappen opzij is eigenlijk hetzelfde als hoeveel verschil er zit tussen de x-waarde van het rechtse punt en de x-waarde van het linkse punt. We zullen de x-waarde van het rechtse punt $\orange{x_2}$ noemen en de x-waarde van het linkse punt $\orange{x_1}$ :

\text{rico} = \frac{\green{\text{hoeveel we stijgen of dalen}}}{\orange{x_2} - \orange{x_1}}

Hoeveel we stijgen of dalen, is dan weer hetzelfde als hoeveel verschil er zit tussen de y-waarde van het rechtse punt en de y-waarde van het linkse punt. De y-waarde van het rechtse punt is hetzelfde als de functiewaarde van $x_2$ . Die kunnen we dus schrijven als $\green{f(x_2)}$ . Zo is ook de y-waarde van het linkse punt hetzelfde als de functiewaarde van $x_1$ , of $\green{f(x_1)}$ :

\text{rico} = \frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{\orange{x_2} - \orange{x_1}}}

Dit is de formule voor het berekenen van de rico van een eerstegraadsfunctie $f(x)$ !

Het differentiequotiënt is ook een rico

Wanneer we de formule voor de rico van een eerstegraadsfunctie eens goed bekijken, zien we toch wel opvallende gelijkenissen met de formule voor het differentiequotiënt:

Formule voor de rico van een eerstegraadsfunctie	Formule voor het differentiequotiënt
$\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{\orange{x_2} - \orange{x_1}}}$	$\frac{\green{f(x_2)} - \green{f(x_1)}}{\orange{\orange{x_2} - \orange{x_1}}}$

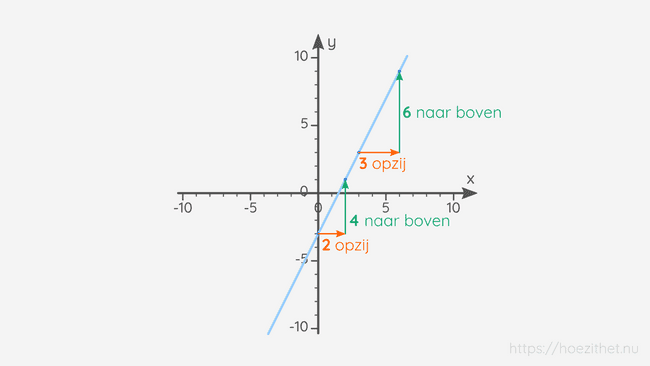
De formule voor de rico en het differentiequotiënt zijn identiek dezelfde! Wat betekent dat? Wel, wanneer we een differentiequotiënt berekenen, berekenen we eigenlijk ook de rico van de eerstegraadsfunctie (of de rechte) die door de punten met coördinaten $(\orange{x_1}, \green{f(x_1)})$ en $(\orange{x_2}, \green{f(x_2)})$ gaat!

De limiet zorgt voor een raaklijn

In onze les over de afgeleide in een punt zagen we dat we de afgeleide van een functie in $x = a$ vinden door het differentiequotiënt te berekenen waarbij we $\Delta x$ (of $x_2 - x_1$ ) naar $0$ laten gaan:

f'(a) = \lim_{\Delta x \to 0} \frac{ \green{f(a + \Delta x)} - \green{f(a)} }{\orange{\Delta x}}

Als $\Delta x$ naar $0$ gaat, betekent het dat de twee punten waartussen we het differentiequotiënt berekenen steeds dichter en dichter bij elkaar komen.

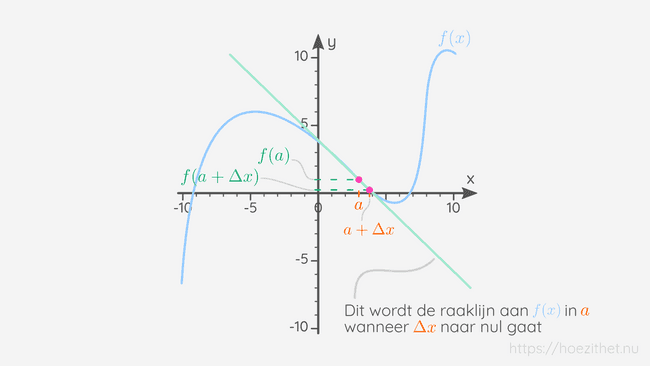
Wat gebeurt er nu wanneer we telkens een lijn zouden trekken door twee punten op een functie die steeds dichter en dichter bij elkaar komen? We zien op de grafiek dat die lijn een raaklijn aan de grafiek is wanneer de twee punten héél dicht bij elkaar zijn.

De limiet in de formule van de afgeleide zorgt er dus voor dat we het differentiequotiënt gaan berekenen tussen twee punten die op de raaklijn van de functie in $x = a$ liggen.

De afgeleide is de rico van de raaklijn in $x = a$

In de voorgaande paragrafen hebben we twee dingen geleerd:

Het berekenen van het differentiequotiënt tussen twee punten $(\orange{x_1}, \green{f(x_1)})$ en $(\orange{x_2}, \green{f(x_2)})$ is hetzelfde als het berekenen van de rico van de eerstegraadsfunctie die door de punten met coördinaten $(\orange{x_1}, \green{f(x_1)})$ en $(\orange{x_2}, \green{f(x_2)})$ gaat
Het berekenen van de limiet van $\Delta x$ naar $0$ in de formule van de afgeleide van een functie in $x = a$ , zorgt ervoor dat we het differentiequotiënt berekenen tussen twee punten die op de raaklijn aan de functie in $x = a$ liggen

De formule van een afgeleide in een punt combineert die limiet en dat differentiequotiënt:

f'(a) = \lim_{\Delta x \to 0} \frac{ \green{f(a + \Delta x)} - \green{f(a)} }{\orange{\Delta x}}

Het differentiequotiënt berekent een rico tussen twee punten die door de limiet héél dicht bij elkaar worden gebracht. Omdat die twee punten een raaklijn gaan vormen, berekenen we met de afgeleide in $x = a$ dus de rico van de raaklijn in $x = a$ .