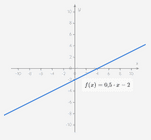
Wat is een functie van de eerste graad?

Wanneer je de eerste keer leert over functies, kan dat allemaal nogal abstract klinken. Op het eerste zicht is het niet zo duidelijk waarom zoiets bestaat en hoe iemand ooit op het idee is gekomen om dat te verzinnen... 🤨

Dat gevoel is heel normaal en is zelfs vollédig terecht, want functies zijn abstract. En dat is precies waarom ze zo interessant en héél breed toepasbaar zijn! 🙌 Functies, en zo ook eerstegraadsfuncties, zijn een mooi voorbeeld van het hele idee achter wiskunde: we willen een onderliggende werking (die bij vele toepassingen hetzelfde is) blootleggen en bestuderen. Door de eigenschappen van die onderliggende werking te ontdekken, ontdekken we dan meteen ook eigenschappen van àl die toepassingen! 💃

Voorbeelden van eerstegraadsfuncties

Laat ons dit even illustreren aan de hand van twee voorbeelden... 👨‍🎨

Voorbeeld 1: Dirk naar het festival 🤘

Dirk gaat volgende week naar een muziekfestival en is in onderhandeling met Maria over hoeveel geld hij mag meenemen.

Dirk drinkt al eens graag een goed glas melk wanneer hij op een festivalweide staat. Hij wil dan ook liefst zoveel mogelijk glazen melk kunnen drinken.

Een toegangsticket voor het festival bedraagt €25 en voor een glas melk vraagt het festival €3. Dirk zou graag willen weten welk budget hij met Maria moet onderhandelen om een bepaald aantal glazen melk te kunnen drinken op het festival.

We weten dat Dirk al minstens €25 nodig zal hebben om het toegangsticket te kunnen betalen. Maar dan heeft hij nog geen enkel glas melk natuurlijk. Voor elk glas melk dat hij wil drinken, komt er €3 bovenop die €25. Het budget dat hij moet onderhandelen is dus €25 plus het aantal glazen melk dat hij wil drinken maal de prijs van een glas melk:

Als Dirk bijvoorbeeld $\orange{5}$ glazen melk wil drinken, dan zal hij een budget van $(\euro 3\cdot \orange{5}) + \euro 25 = \euro 40$ nodig hebben.

We kunnen wat schrijfwerk besparen door de formule als volgt te schrijven:

Voorbeeld 2: Maria eet pralines

Maria is dol van pralines. Ze toonde dan ook met plezier haar groot hart toen de lokale gymclub haar vorige week vroeg om hen te steunen door chocolade zeevruchten te kopen. 🤤 Ze kocht meteen een grote doos van $1~\si{kg}$. Zo'n doos bevat 64 pralines.

Maria weet natuurlijk wel dat ze die hele doos best niet op één dag naar binnen speelt. Ze heeft dan ook besloten om elke dag slechts 4 pralines te eten. Na enkele dagen vraagt ze zich af hoeveel pralines er nog in de doos zitten. Hoe kan ze dit berekenen?

Er zitten oorspronkelijk $64$ pralines in de doos en er gaan er iedere dag $4$ uit. Het aantal pralines dat op een bepaalde dag nog in de doos zit, is dus gelijk aan $64$ min het aantal dagen maal $4$:

Dit kunnen we herschrijven als:

Dit is dan weer hetzelfde als:

Na bijvoorbeeld $\orange{5}$ dagen zullen er nog $(-4\cdot \orange{5}) + 64 = 44$ pralines in de doos zitten.

We kunnen weer wat schrijfwerk besparen door de formule als volgt te schrijven:

Voorbeeld 3: Bevroren soep ontdooien

Maria en Dirk maken regelmatig een grote kom soep die ze verdelen in verschillende potjes om in te vriezen. Zo'n potje hoeven ze dan enkel terug op te warmen om te kunnen genieten van een heerlijke en gezonde portie soep.

Wanneer ze zo'n portie uit de diepvriezer halen, heeft de soep een temperatuur van $-18\deg\si{C}$. Ze plaatsen de portie soep in de microgolfoven. Deze laat de temperatuur van de soep stijgen met $6\deg\si{C}$ per minuut. Wat is de temperatuur van de soep nadat die een bepaald aantal minuten in de microgolfoven heeft gestaan?

De temperatuur van de soep bedraagt in het begin $-18\deg \si{C}$. Iedere minuut komt daar $6\deg \si{C}$ bij. De temperatuur van de soep is dus gelijk aan $-18\deg \si{C}$ plus het aantal minuten maal $6\deg \si{C}$:

Dit kunnen we ook schrijven als:

Dat is dan weer hetzelfde als:

Of, in symbolen:

Algemene vorm van een eerstegraadsfunctie

Bij het eerste voorbeeld vonden we de volgende uitdrukking:

Bij het tweede voorbeeld kwamen we uit bij:

Bij het derde voorbeeld kregen we:

Als je deze uitdrukkingen naast elkaar legt, zie je dat ze een heel gelijkaardige vorm hebben. We rekenen telkens een $y$ uit door een $x$ te vermenigvuldigen met een bepaald getal en daar dan een ander (al dan niet negatief) getal bij op te tellen. Als we het eerste getal vervangen door een $m$ en het tweede getal door een $q$, dan krijgen we:

Oefening NaN

Waaraan zijn $m$ en $q$ gelijk in $y = -7\cdot x+6$?

$$\begin{aligned} m &= -7\\ q &= 6\\ \end{aligned}$$

$$\begin{aligned} m &= 6\\ q &= -7\\ \end{aligned}$$

$$\begin{aligned} m &= 7\\ q &= 6\\ \end{aligned}$$

$$\begin{aligned} m &= -7\\ q &= -6\\ \end{aligned}$$

$$\begin{aligned} m &= 7\\ q &= -6\\ \end{aligned}$$

Vorige

Volgende

Oefening NaN

Waaraan zijn $m$ en $q$ gelijk in $y = 4\cdot x$?

$$\begin{aligned} m &= 4\\ q &= 0\\ \end{aligned}$$

$$\begin{aligned} m &= 0\\ q &= 4\\ \end{aligned}$$

$$\begin{aligned} m &= -4\\ q &= 0\\ \end{aligned}$$

Vorige

Volgende

Oefening NaN

Waaraan zijn $m$ en $q$ gelijk in $y = 9\cdot x$?

$$\begin{aligned} m &= 9\\ q &= 0\\ \end{aligned}$$

$$\begin{aligned} m &= 0\\ q &= 9\\ \end{aligned}$$

$$\begin{aligned} m &= -9\\ q &= 0\\ \end{aligned}$$

Vorige

Volgende

Oefening NaN

Waaraan zijn $m$ en $q$ gelijk in $y = -9$?

$$\begin{aligned} m &= 0\\ q &= -9\\ \end{aligned}$$

$$\begin{aligned} m &= -9\\ q &= 0\\ \end{aligned}$$

$$\begin{aligned} m &= 0\\ q &= 9\\ \end{aligned}$$

Vorige

Volgende

Oefening NaN

Waaraan zijn $m$ en $q$ gelijk in $y = -5\cdot x-2$?

$$\begin{aligned} m &= -5\\ q &= -2\\ \end{aligned}$$

$$\begin{aligned} m &= -2\\ q &= -5\\ \end{aligned}$$

$$\begin{aligned} m &= 5\\ q &= -2\\ \end{aligned}$$

$$\begin{aligned} m &= -5\\ q &= 2\\ \end{aligned}$$

$$\begin{aligned} m &= 5\\ q &= 2\\ \end{aligned}$$

Vorige

Klaar

Je behaalde:

0/5

Begin opnieuw

Toon oplossing

Er zijn talloze situaties waar we een $y$ kunnen uitrekenen met een $x$ via $y=m x + q$. Dat komt zelfs zo vaak voor dat we er een speciale naam aan geven: eerstegraadsfuncties.

Merk op dat we vaak in plaats van die $y$ ook wel $f(x)$ schrijven:

Met die $x$ tussen haakjes achter de $f$ bedoelen we dan dat de functie $f$ afhangt van $x$ (en niet dat $f$ vermenigvuldigd wordt met $x$!). We noemen $f(x) = m x + q$ het voorschrift van $f$. We definiëren een eerstegraadsfunctie dan als volgt:

We gebruiken de naam eerstegraadsfunctie omdat de hoogste macht van $x$ in $mx + q$ gelijk is aan $1$. We noemen $mx + q$ ook wel een veelterm van de eerste graad in $x$.

Oefening NaN

Is $f(x) = -5 + x$ een eerstegraadsfunctie in $x$? Zo ja, waaraan zijn $m$ en $q$ gelijk? (Noteer dit zelf op papier)

JaNeen

Vorige

Volgende

Oefening NaN

Is $f(x) = 3$ een eerstegraadsfunctie in $x$? Zo ja, waaraan zijn $m$ en $q$ gelijk? (Noteer dit zelf op papier)

JaNeen

Vorige

Volgende

Oefening NaN

Is $f(x) = (2 x + 1)^{-1}$ een eerstegraadsfunctie in $x$? Zo ja, waaraan zijn $m$ en $q$ gelijk? (Noteer dit zelf op papier)

JaNeen

Vorige

Volgende

Oefening NaN

Is $f(x) = \frac{x + 2}{3}$ een eerstegraadsfunctie in $x$? Zo ja, waaraan zijn $m$ en $q$ gelijk? (Noteer dit zelf op papier)

JaNeen

Vorige

Volgende

Oefening NaN

Is $f(x) = 0x - 3$ een eerstegraadsfunctie in $x$? Zo ja, waaraan zijn $m$ en $q$ gelijk? (Noteer dit zelf op papier)

JaNeen

Vorige

Klaar

Je behaalde:

0/5

Begin opnieuw

Toon oplossing

Intuïtie achter functies van de eerste graad

Hoe komt het dat de voorbeelden van Dirk die naar een festival gaat, van Maria die pralines eet en van bevroren soep die opgewarmd wordt allemaal leiden tot een functie van de eerste graad? Wel, per extra glas melk kwam er een vast bedrag van €3 bij het *budget bij; per extra dag ging er een vast aantal pralines uit de doos; en per extra minuut kwam er een vast aantal graden Celsius bij de begintemperatuur bij. Elke situatie waar er voor elke extra $x$ een vast aantal weggaat of bijkomt bij een beginaantal kunnen we wiskundig beschrijven met een eerstegraadsfunctie. Het vast aantal dat per $x$ weggaat of bijkomt, is $m$. Het beginaantal (wanneer $x = 0$), is $q$.

Je ziet dat we met onze eerstegraadsfunctie inderdaad de onderliggende werking (waar we het in het begin van de les over hadden) blootleggen.

Een functie van de eerste graad herkennen en omzetten naar $y = mx + q$

Elke situatie waar er een vast aantal per $x$ weggaat of bijkomt bij een beginaantal (wanneer $x = 0$), gedraagt zich als een eerstegraadsfunctie. In het volgende kader vatten we samen hoe je in een opgave kan herkennen dat het om een eerstegraadsfunctie gaat en hoe je vervolgens het voorschrift kan vinden van die eerstegraadsfunctie.

Probeer het voorgande nu zelf toe te passen op de volgende oefeningen.

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

Het totaalbedrag $y$ dat je moet betalen na een taxirit van $x$ minuten. Iedere minuut komt er 30 eurocent bij het starttarief van 3 euro bij.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Volgende

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

De oppervlakte $y$ van een vierkant met zijde $x$.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Volgende

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

De hoek $y$ die de grote wijzer van een horloge heeft afgelegd na $x$ kwartieren. Per kwartier vergroot de hoek met $90\deg$.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Volgende

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

De winst $y$ die je maakt bij een cakeverkoop nadat je $x$ sneden cake hebt verkocht. Je kocht in de winkel zelf voor €25 aan cakes en vraagt 50 eurocent voor iedere snede cake.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Volgende

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

De omtrek $y$ van een cirkel met straal $x$.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Volgende

Oefening NaN

Is $y$ een eerstegraadsfunctie van $x$?

De afstand $y$ die een voorwerp in vrije val heeft afgelegd na $x$ seconden. De snelheid van het voorwerp begint bij $0~\si{m/s}$ en verhoogt iedere seconde met $9{,}81~\si{m/s}$.

$y$ is geen eerstegraadsfunctie van $x$.$y$ is wel een eerstegraadsfunctie van $x$.

Vorige

Klaar

Je behaalde:

0/6

Begin opnieuw

Toon oplossing

Samengevat

Hoe duidelijk vond je deze les?

Niet duidelijk

Redelijk duidelijk

Heel duidelijk

Volgende les: De grafiek van een eerstegraadsfunctie 👉

Vragen en reacties