Afgeleiden

In deze les leggen we het differentiequotiënt uit aan de hand van de snelheid van een racewagen. We beginnen met het intuïtief opbouwen van een algemene formule om snelheid te berekenen en maken zo een intuïtieve overstap naar de formule voor het differentiequotiënt.

Met afgeleiden berekenen we ogenblikkelijke veranderingen. In deze les leren we de formule om zo'n afgeleide te berekenen. We bouwen stap per stap op naar de definitie vertrekkend van het differentiequotiënt. Zo begrijp je aan het einde van de les helemaal waar de definitie van afgeleiden vandaan komt.

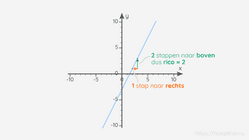
Door eens goed naar de definitie van een afgeleide te kijken, kunnen we inzien dat deze eigenlijk gelijk is aan een richtingscoëfficiënt. Meer bepaald is de afgeleide in een punt a de rico van de raaklijn aan de grafiek van de functie in a. Dat is een hele mond vol. Maar gelukkig bouwen we in deze les stap per stap en met behulp van veel illustraties op naar deze interpretatie van een afgeleide.

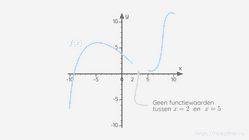
Een functie is niet altijd in ieder punt afleidbaar. In deze les leren we wat de voorwaarden zijn waar een functie aan moet voldoen opdat de functie afleidbaar zou zijn in een bepaald punt x = a.

In deze les leren we hoe we de afgeleide van een functie kunnen berekenen. De afgeleide van een functie is een functievoorschrift waarmee we de afgeleide voor alle mogelijke x-waarden van de functie kunnen vinden. We leggen dit uit aan de hand van de afgeleide van een tweedegraadsfunctie.

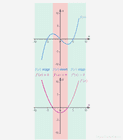
De afgeleide van een functie is zelf ook een functie en heeft dus een grafiek. In deze les leren we hoe je het verband kan zien tussen de grafiek van de afgeleide van een functie en de grafiek van de functie zelf.