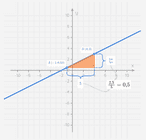
De grafiek van een eerstegraadsfunctie
Stel dat de volgende eerstegraadsfunctie gegeven is:
Door enkele x-waarden in te vullen in dit functievoorschrift, kunnen we de bijhorende functiewaarden berekenen. Als we bijvoorbeeld invullen, dan vinden we
Bij de x-waarde hoort dus een functiewaarde van . Het punt met coördinaten ligt daarom op de grafiek van de functie :
We kunnen andere willekeurige x-waarden invullen in de gegeven functie . Onze resultaten zetten we in een waardentabel:
| x-waarde | functiewaarde |
|---|---|
| -8 | -6 |
| -2 | -3 |
| 2 | -1 |
| 6 | 1 |
De verschillende punten lijken op eenzelfde rechte lijn te liggen. Dit is geen toeval: de punten op de grafiek van een eerstegraadsfunctie liggen altijd op een rechte lijn. Als je voor nog veel meer x-waarden de y-waarde zou berekenen, zal je zien dat al die punten ook op diezelfde lijn liggen. De grafiek van de functie is:
De punten op de grafiek van een eerstegraadsfunctie liggen altijd op een rechte lijn.
Invloed van op de grafiek
We gaan nu eens bekijken wat er met de grafiek van een eerstegraadsfunctie gebeurt als we de in het functievoorschrift veranderen. Herinner je dat het getal is waarmee wordt vermenigvuldigd in het voorschrift.
Verander de waarde van door het bolletje van de slider heen en weer te schuiven. Gebruik je bevindingen om onderstaande oefeningen op te lossen.
We zien dat het teken van bepaalt of de functie zal stijgen of dalen en dat de absolute waarde van de steilheid bepaalt. We zeggen daarom dat de richting bepaalt van de functie en noemen ook wel de richtingscoëfficiënt of rico. De volgende les zoomt wat dieper in op de richtingscoëfficiënt.
Invloed van op de grafiek
We bekijken nu ook wat er met de grafiek gebeurt wanneer van waarde verandert. Herinner je dat het getal is dat bij wordt opgeteld in het voorschrift.
Verschuif het bolletje op de slider van en gebruik opnieuw je bevindingen om onderstaande oefeningen op te lossen.
Je merkt dat een invloed heeft op hoe hoog de grafiek van de functie ligt. Wanneer verandert, verandert het snijpunt van de grafiek en de y-as. Meer zelfs: het snijpunt van de grafiek en de y-as heeft altijd als y-coördinaat. De grafiek van een functie snijdt de y-as dus altijd in het punt .
Samengevat
De grafiek van een functie stijgt wanneer en daalt wanneer . Hoe groter de absolute waarde van , hoe steiler de grafiek.
De grafiek van een functie snijdt de y-as in .