De richtingscoëfficiënt of rico

Inhoud

De rico van een rechte door twee punten berekenen
De rico snel aflezen op een grafiek
Samengevat

Het voorschrift van een eerstegraadsfunctie ziet er als volgt uit:

f(x) = mx + q

We leerden in de vorige les al dat de waarde van $m$ de richting bepaalt van de grafiek van $f$ :

Als $m\gt 0$ , dan is de grafiek van $f$ stijgend;
Als $m\lt 0$ , dan is de grafiek van $f$ dalend;
Als $m = 0$ , is $f$ geen eerstegraadsfunctie maar een constante functie en is de grafiek van $f$ vlak;
Hoe groter de absolute waarde van $m$ , hoe steiler de grafiek van $f$ .

We noemen $m$ de richtingscoëfficiënt of rico van $f$ : richting- omdat het de richting bepaalt van de grafiek van $f$ en -coëfficiënt omdat het een getal is dat vermenigvuldigd wordt met $x$ (en dus een coëfficiënt is van $x$ ).

In deze les leren we hoe je de rico kan vinden in de volgende situaties:

wanneer er twee punten zijn gegeven die op de grafiek van $f$ liggen;
wanneer de grafiek van $f$ is gegeven.

De rico van een rechte door twee punten berekenen

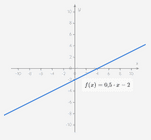
Hieronder staat de grafiek van de functie

f(x) = 0{,}5 x + 1

We hebben twee willekeurige punten $A$ en $B$ aangeduid die op de grafiek van $f$ liggen. De twee punten vormen de schuine zijde van een rechthoekige driehoek, waarvan de rechthoekszijden evenwijdig zijn met de x- en y-as. We duiden de lengte aan van elke rechthoekszijde van deze loodrechte driehoek.

Met behulp van de sliders kan je zelf de x-waarde van $A$ en $B$ veranderen en zie je de rechthoekige driehoek en de lengten van de rechthoekszijden mee veranderen.

x_1 = -1

x_2 = 4

We delen de lengte van de verticale rechthoekszijde door de lengte van de horizontale rechthoekszijde. Je ziet dat deze deling altijd gelijk is aan de richtingscoëffiënt van $f$ ! Het maakt niet uit welke twee punten je kiest op de grafiek, de verhouding van de lengten van de rechthoekszijden zal altijd gelijk zijn aan $0{,}5$ : de rico.

We kunnen de rico van een functie dus vinden door het quotiënt te berekenen van de lengten van die rechthoekszijden:

m = \frac{\text{lengte vert. rechthoekszijde}}{\text{lengte horiz. rechthoekszijde}}

Als $A$ en $B$ de coördinaten $(x_1, y_1)$ en $(x_2, y_2)$ hebben, dan zal

de verticale rechthoekszijde een lengte hebben die gelijk is aan $y_2 - y_1$ ;
de horizontale rechthoekszijde een lengte hebben die gelijk is aan $x_2 - x_1$ .

We kunnen de lengtes in onze formule voor $m$ dus uitdrukken met de coördinaten van de twee punten:

m = \frac{y_2 - y_1}{x_2 - x_1}

Met deze formule kunnen we de rico van $f$ berekenen als we de coördinaten kennen van twee punten die op de grafiek van $f$ liggen.

💡 De rico van een rechte door twee punten berekenen

Gegeven de punten $(x_1, y_1)$ en $(x_2, y_2)$ , dan is

m = \frac{y_2 - y_1}{x_2 - x_1}

de richtingscoëfficiënt van de eerstegraadsfunctie die door beide punten loopt.

Merk op dat wanneer de functie daalt, $y_2 - y_1 \lt 0$ zodat ook $m\lt 0$ :

x_1 = -1

x_2 = 4

Oefening NaN

Wat is het functievoorschrift van de eerstegraadsfunctie die door de punten

(4;-4)

(-10;-6)

gaat?

(Noteer je antwoord zelf op papier.)

De rico snel aflezen op een grafiek

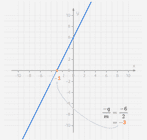
In de vorige paragraaf leerden we dat de rico van de eerstegraadsfunctie die door de punten $(x_1, y_1)$ en $(x_2, y_2)$ gaat, gelijk is aan

m = \frac{y_2 - y_1}{x_2 - x_1}

Stel dat de punten $A(2, 5)$ en $B(3, 8)$ op de grafiek van $f$ liggen. We gaan even enkel de noemer van de breuk invullen:

\begin{aligned} m &= \frac{y_2 - y_1}{3 - 2}\\ &= \frac{y_2 - y_1}{\cancel{1}}\\ &= y_2 - y_1 \end{aligned}

Je ziet dat de noemer van de breuk gelijk is aan $1$ en mag geschrapt worden. Alleen de teller van de breuk blijft over. De rico is voor deze twee punten gewoon gelijk aan $y_2 - y_1$ !

De x-coördinaat van $A$ is $2$ en die van $B$ is $3$ . De punten liggen dus één x-eenheid van elkaar. Daardoor is de noemer van onze breuk ook $1$ en kunnen we de noemer schrappen. Je ziet ook op de grafiek dat wanneer twee punten één x-eenheid van elkaar liggen, de rico altijd gelijk is aan $y_2-y_1$ :

x_1 = 2

m = 3

We kunnen de rico dus ook aflezen op een grafiek door twee punten te kiezen die één x-eenheid van elkaar liggen. Het verschil van hun y-coördinaten ( $y_2 - y_1$ ) is dan gelijk aan de rico.